题目内容
(本小题满分14分)
设函数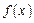 的定义域为R,当x<0时,
的定义域为R,当x<0时,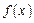 >1,且对任意的实数x,y∈R,有
>1,且对任意的实数x,y∈R,有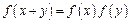 .
.
(1)求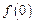 ,判断并证明函数
,判断并证明函数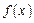 的单调性;
的单调性;
(2)数列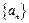 满足
满足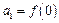 ,且
,且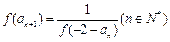 ,
,
①求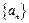 通项公式;
通项公式;
②当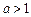 时,不等式
时,不等式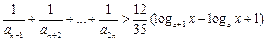 对不小于2的正整数
对不小于2的正整数
恒成立,求x的取值范围.
设函数
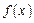 的定义域为R,当x<0时,
的定义域为R,当x<0时,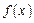 >1,且对任意的实数x,y∈R,有
>1,且对任意的实数x,y∈R,有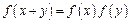 .
.(1)求
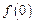 ,判断并证明函数
,判断并证明函数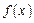 的单调性;
的单调性;(2)数列
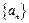 满足
满足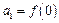 ,且
,且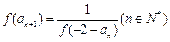 ,
,①求
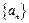 通项公式;
通项公式;②当
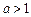 时,不等式
时,不等式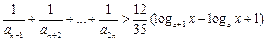 对不小于2的正整数
对不小于2的正整数恒成立,求x的取值范围.
f(x)在R上减函数
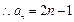 (1,+∞)
(1,+∞)
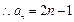 (1,+∞)
(1,+∞)解:(1) 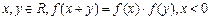 时,f(x)>1;
时,f(x)>1;
令x=-1,y=0则f(-1)=f(-1)f(0)∵f(-1)>1,
∴f(0)="1" . ……………………………2分
若x>0,则f(x-x)=f(0)=f(x)f(-x)故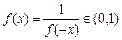 ,
,
故x∈R f(x)>0.…………………………………………………4分
任取x1<x2,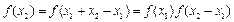 ,
,
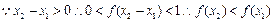 ,
,
故f(x)在R上减函数.……………………………6分
(2) ①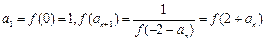 ,…………8分
,…………8分
由f(x)单调性得 an+1=an+2 , 故{an}等差数列 ,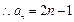 .………………9分
.………………9分
②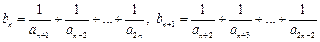 ,
,
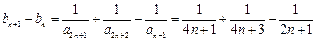
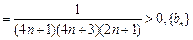 是递增数列.………………………11分
是递增数列.………………………11分
当n≥2时,
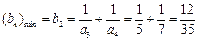 ,
,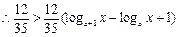 ,……………………………12分
,……………………………12分
即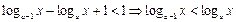 .
.
而a>1,∴x>1,
故x的取值范围(1,+∞).……………………………14分
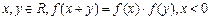 时,f(x)>1;
时,f(x)>1;令x=-1,y=0则f(-1)=f(-1)f(0)∵f(-1)>1,
∴f(0)="1" . ……………………………2分
若x>0,则f(x-x)=f(0)=f(x)f(-x)故
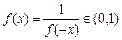 ,
,故x∈R f(x)>0.…………………………………………………4分
任取x1<x2,
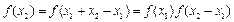 ,
,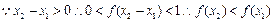 ,
,故f(x)在R上减函数.……………………………6分
(2) ①
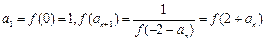 ,…………8分
,…………8分由f(x)单调性得 an+1=an+2 , 故{an}等差数列 ,
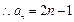 .………………9分
.………………9分②
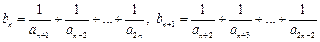 ,
,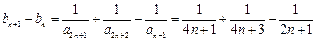
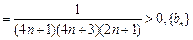 是递增数列.………………………11分
是递增数列.………………………11分
|

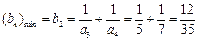 ,
,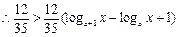 ,……………………………12分
,……………………………12分即
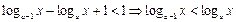 .
.而a>1,∴x>1,
故x的取值范围(1,+∞).……………………………14分

练习册系列答案
相关题目
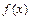 是定义在
是定义在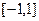 上的奇函数,当
上的奇函数,当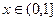 时,
时,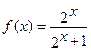
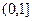 上的单调性,并用单调性的定义证明;
上的单调性,并用单调性的定义证明;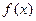 的值域.
的值域.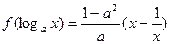 ,其中
,其中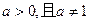 。
。 ;
;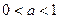 时,判别
时,判别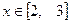 时
时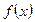 的最小值;
的最小值;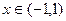 时恒有
时恒有 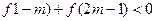 ,求
,求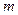 的取值范围。
的取值范围。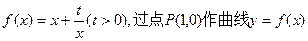 的两条切线PM、PN,切点分
的两条切线PM、PN,切点分 别为M、N.
别为M、N.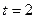 时,求函数
时,求函数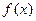 的单调
的单调 递增区间;
递增区间;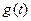 ,试求函数
,试求函数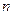 ,在区间
,在区间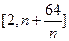 内,总存在m+1个数
内,总存在m+1个数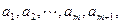 使得不等式
使得不等式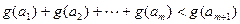 成立,求m的最大值.
成立,求m的最大值.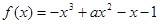 在
在 上是单调函数,则实数
上是单调函数,则实数 的取值范围是
的取值范围是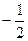 <m<
<m<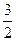
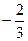 <m<
<m<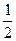

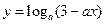 在
在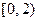 上是关于x的减函数,则实数a的取值范围为 ▲ .
上是关于x的减函数,则实数a的取值范围为 ▲ .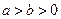 ,那么
,那么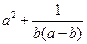 的最小值是 。
的最小值是 。 数的原有运算法则中,我们补充定义新运算“
数的原有运算法则中,我们补充定义新运算“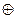 ”如下:当
”如下:当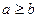 时,
时,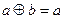 ;当
;当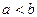
 时,
时,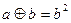 。则函数
。则函数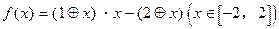 的最大值等于(“·”和“-”仍为通常的乘法和减法)
的最大值等于(“·”和“-”仍为通常的乘法和减法)  ( )
( )