题目内容
(本小题满分11分)已知
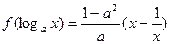 ,其中
,其中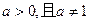 。
。(1)求
 ;
;(2)
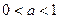 时,判别
时,判别 的单调性并求
的单调性并求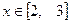 时
时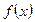 的最小值;
的最小值;(3)对于
 ,当
,当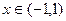 时恒有
时恒有 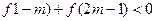 ,求
,求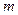 的取值范围。
的取值范围。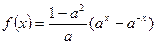
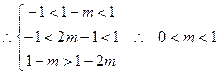
(1)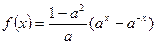
(2)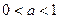 时,
时, 是单调减函数,
是单调减函数,
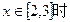
 的最大值是
的最大值是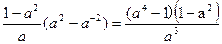
(3)易证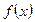 是奇函数,且是增函数,
是奇函数,且是增函数,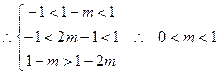
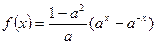
(2)
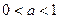 时,
时, 是单调减函数,
是单调减函数,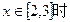
 的最大值是
的最大值是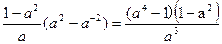
(3)易证
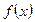 是奇函数,且是增函数,
是奇函数,且是增函数,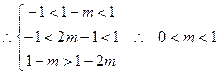

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
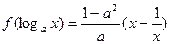 ,其中
,其中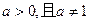 。
。 ;
;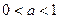 时,判别
时,判别 的单调性并求
的单调性并求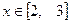 时
时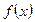 的最小值;
的最小值; ,当
,当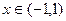 时恒有
时恒有 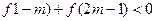 ,求
,求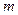 的取值范围。
的取值范围。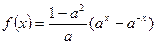
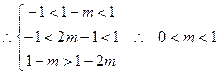
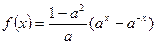
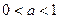 时,
时, 是单调减函数,
是单调减函数,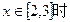
 的最大值是
的最大值是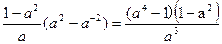
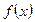 是奇函数,且是增函数,
是奇函数,且是增函数,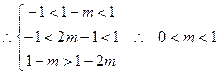

 阅读快车系列答案
阅读快车系列答案