题目内容
6．在ABC中，角A，B，C所对边为a，b，c，若$\frac{a}{cosA}$=$\frac{b}{cosB}$=$\frac{c}{cosC}$，则△ABC是等边三角形．分析 由已知可得：a=$\frac{bcosA}{cosB}$，又由正弦定理可得：a=$\frac{bsinA}{sinB}$，从而$\frac{bcosA}{cosB}$=$\frac{bsinA}{sinB}$，整理可得bsin（B-A）=0，结合A，B的范围可得B=A，同理解得：B=C，从而得解．
解答 解：∵$\frac{a}{cosA}$=$\frac{b}{cosB}$，可得：a=$\frac{bcosA}{cosB}$，
又∵由正弦定理可得：a=$\frac{bsinA}{sinB}$，
∴$\frac{bcosA}{cosB}$=$\frac{bsinA}{sinB}$，整理可得：bcosAsinB-bsinAcosB=bsin（B-A）=0，
∵0＜A＜π，0＜B＜π，解得-π＜B-A＜π，
∴解得B-A=0，即B=A，
同理解得：B=C，
故三角形为等边三角形．
故答案为：等边．
点评 本题主要考查了正弦定理，正弦函数的图象和性质的应用，熟练掌握正弦定理和正弦函数的图象和性质是解题的关键，属于基础题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
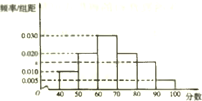某校随机抽取20名学生在一次知识竞赛中的成绩（均为整数），并绘制频率分布直方图（如图所示），其中样本数据分组区间为：[40，50）、[50，60）、[60，70）、[70，80）、[80，90），[90，100]．