题目内容
17.若二项式${(3x-\frac{1}{x})^n}$的展开式的系数之和为64,则展开式中常数项为-540.分析 根据二项式展开式的系数和求出n的值,再利用展开式的通项公式求出常数项.
解答 解:二项式${(3x-\frac{1}{x})^n}$的展开式的系数之和为64,
即2n=64,
解得n=6;
∴${(3x-\frac{1}{x})}^{6}$展开式中通项为
Tr+1=${C}_{6}^{r}$•(3x)6-r•${(-\frac{1}{x})}^{r}$=(-1)r•${C}_{6}^{r}$•36-r•x6-2r,
令6-2r=0,
解得r=3,
∴常数项为T3+1=(-1)3•${C}_{6}^{3}$•33=-540.
故答案为:-540.
点评 本题考查了二项式定理的灵活应用问题,也考查了逻辑推理与计算能力,是基础题目.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
2.已知{an}为等差数列,且a3=6,a4=7,则a10=( )
| A. | 1 | B. | 3 | C. | 10 | D. | 13 |
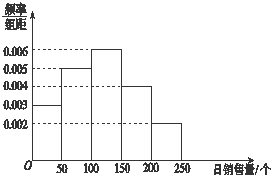 一家企业据以往某种新产品的销售记录,绘制了日销售量的频率分布直方图,如图所示.由频率分布直方图,估计这种新产品的日销售量的中位数为117.(结果保留整数)
一家企业据以往某种新产品的销售记录,绘制了日销售量的频率分布直方图,如图所示.由频率分布直方图,估计这种新产品的日销售量的中位数为117.(结果保留整数)