题目内容
【题目】设函数f(x)= ![]() ,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
A.p假q真
B.p假q假
C.p真q真
D.p真q假
【答案】C
【解析】解:作出函数f(x)= ![]() 的图象如图,
的图象如图,
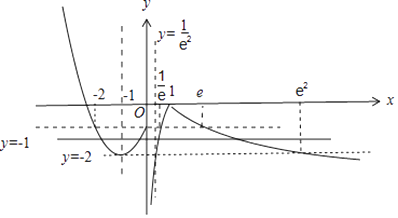
不妨设a<b<c<d,图中实线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈(﹣2,﹣1],
则a,b是x2+2x﹣m﹣1=0的两根,∴a+b=﹣2,ab=﹣m﹣1,
∴ab∈[0,1),且lnc=m,lnd=﹣m,
∴ln(cd)=0,
∴cd=1,
∴abcd∈[0,1),故①正确;
由图可知,c∈( ![]() ],
],
又∵cd=1,a+b=﹣2,
∴a+b+c+d=c+ ![]() ﹣2,在(
﹣2,在( ![]() ,
, ![]() ]是递减函数,
]是递减函数,
∴a+b+c+d∈[e+ ![]() ﹣2,e2+
﹣2,e2+ ![]() ﹣2),故②正确.
﹣2),故②正确.
∴p真q真.
故选:C.
画出函数f(x)=的图象,根据a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),令a<b<c<d,根据对数的运算性质,及c,d的取值范围得到abcd的取值范围,再利用对勾函数的单调性求出a+b+c+d的范围得答案.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?