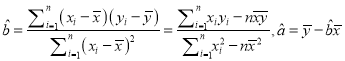题目内容
【题目】设函数f(x)=(x+1)lnx﹣a(x﹣1).
(1)若函数f(x)在x=e处的切线与y轴相交于点(0,2﹣e),求a的值;
(2)当1<x<2时,求证: ![]() >
> ![]() ﹣
﹣ ![]() .
.
【答案】
(1)解:f′(x)=lnx+ ![]() +1﹣a,x∈(0,+∞)
+1﹣a,x∈(0,+∞)
由题意可知: ![]() =f′(e),
=f′(e),
整理得:e+1﹣a(e﹣1)﹣(2﹣e)=e(1+ ![]() +1﹣a),解得a=2
+1﹣a),解得a=2
(2)证明:(2)当a=2时,f(x)=(x+1)lnx﹣2(x﹣1),
f′(x)=lnx+ ![]() ﹣1,f″(x)=
﹣1,f″(x)= ![]() >0,
>0,
∴f′(x)在(1,2)递增,∴f′(x)>f′(1)=0,
∴f(x)在(1,2)上是增函数,
∴f(x)>f(1)=0,即(x+1)lnx>2(x﹣1),
∴ ![]() <
< ![]() ,①
,①
∵1<x<2,
∴0<2﹣a<1, ![]() >1,
>1,
∴ ![]() <
< 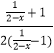 =
= ![]() ,
,
即﹣ ![]() <
< ![]() ,②
,②
①+②得: ![]() ﹣
﹣ ![]() <
< ![]() +
+ ![]() =
= ![]()
【解析】(1)求函数的导数,根据导数的几何意义即可求出函的切线斜率,即可求得a的值;(2)a=2时,f(x)=(x+1)lnx﹣2(x﹣1),得到f(x)在(1,2)上是增函数,可知(x+1)lnx>2(x﹣1),即 ![]() <
< ![]() 利用函数的单调性,求得﹣
利用函数的单调性,求得﹣ ![]() <
< ![]() ,根据对数函数的运算即可证明不等式成立.
,根据对数函数的运算即可证明不等式成立.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目