题目内容
【题目】统计表明，家庭的月理财投入
（单位：千元）与月收入
（单位：千元）之间具有线性相关关系．某银行随机抽取5个家庭，获得第
（
）个家庭的月理财投入
与月收入
的数据资料，经计算得
．
（1）求
关于
的回归方程
；
（2）判断
与
之间是正相关还是负相关；
（3）若某家庭月理财投入为5千元，预测该家庭的月收入．
附：回归方程的斜率与截距的最小二乘估计公式分别为：
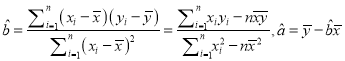，其中
为样本平均值．
【答案】(1) 回归方程为
;(2)正相关；（3）该家庭月理财投入为5千元，则该家庭的月收入约为13.7千元.
【解析】试题分析：⑴由题意求出
， 
，求出回归系数
， 
，写出回归方程；
⑵由回归系数
，判断是正相关；
⑶计算
时
的值，即可预测该家庭的月收入；
解析：（1）由题意知
， 
，
又
， 
，
故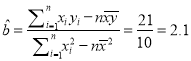
， 
，
故所求回归方程为
；
（2）由于
的值随
值的增加而增加
，故
与
之间是正相关；
（3）将
代入回归方程得
千元，
故若该家庭月理财投入为5千元，则该家庭的月收入约为13.7千元．
新课标快乐提优暑假作业陕西旅游出版社系列答案【题目】《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区，已建成的住宅小区和单位大院逐步打开”，此消息在网上一石激起千层浪．各种说法不一而足，为了了解居民对“开放小区”认同与否，从[25，55]岁人群中随机抽取了n人进行问卷调查，得如下数据：
组数 | 分组 | 认同人数 | 认同人数占 |
第一组 | [25，30） | 120 | 0.6 |
第二组 | [30，35） | 195 | p |
第三组 | [35，40） | 100 | 0.5 |
第四组 | [40，45） | a | 0.4 |
第五组 | [45，50） | 30 | 0.3 |
第六组 | [50，55） | 15 | 0.3 |
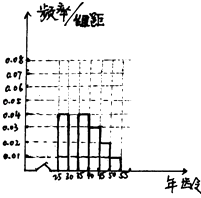
（1）完成所给频率分布直方图，并求n，a，p．
（2）若从[40，45），[45，50）两个年龄段中的“认同”人群中，按分层抽样的方法抽9人参与座谈会，然后从这9人中选2名作为组长，组长年龄在[40，45）内的人数记为ξ，求随机变量ξ的分布列和期望．
