题目内容
【题目】已知数列{an}满足[2﹣（﹣1）n]an+[2+（﹣1）n]an+1=1+（﹣1）n×3n，则a25﹣a1= ．
【答案】300
【解析】解：∵[2﹣（﹣1）n]an+[2+（﹣1）n]an+1=1+（﹣1）n×3n，
∴n=2k（k∈N*），可得：a2k+3a2k+1=1+6k，
n=2k﹣1（k∈N*），可得：3a2k﹣1+a2k=1﹣6k+3，
∴a2k+1﹣a2k﹣1=4k﹣1，
∴a25=（a25﹣a23）+（a23﹣a21）+…+（a3﹣a1）+a1
=（4×12﹣1）+（4×11﹣1）+…+（4×1﹣1）+a1= 
﹣12+a1=300+a1 ．
则a25﹣a1=300，
故答案为：300．
由[2﹣（﹣1）n]an+[2+（﹣1）n]an+1=1+（﹣1）n×3n，当n=2k（k∈N*），可得：a2k+3a2k+1=1+6k，n=2k﹣1（k∈N*），可得：3a2k﹣1+a2k=1﹣6k+3，于是a2k+1﹣a2k﹣1=4k﹣1，利用“累加求和”方法与等差数列的前n项和公式即可得出．
【题目】近年来城市“共享单车”的投放在我国各地迅猛发展，“共享单车”为人们出行提供了很大的便利，但也给城市的管理带来了一些困难，现某城市为了解人们对“共享单车”投放的认可度，对
年龄段的人群随机抽取
人进行了一次“你是否赞成投放共享单车”的问卷调查，根据调查结果得到如下统计表和各年龄段人数频率分布直方图：
组号 | 分组 | 赞成投放的人数 | 赞成投放的人数占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|
（
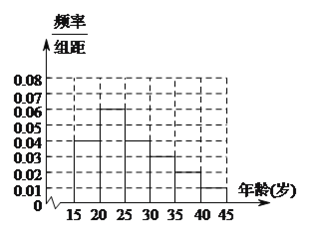
）求
， 
， 
的值．
（
）在第四、五、六组“赞成投放共享单车”的人中，用分层抽样的方法抽取
人参加“共享单车”骑车体验活动，求第四、五、六组应分别抽取的人数．
（
）在（
）中抽取的
人中随机选派
人作为领队，求所选派的
人中第五组至少有一人的概率．
