Question

【题目】在平面直角坐标系xoy中，曲线C的参数方程为 （θ为参数），直线l的参数方程为 （t为参数）以坐标原点O为极点，x轴的正半轴为极轴的极坐标系．
（1）写出直线l的普通方程以及曲线C的极坐标方程；
（2）若直线l与曲线C的两个交点分别为M，N，直线l与x轴的交点为P，求|PM||PN|的值．

Answer 1

【答案】
（1）解：直线l的参数方程为 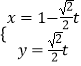（t为参数），消去参数t可得：x+y﹣1=0．

曲线C的参数方程为 （θ为参数），利用平方关系可得：x2+（y﹣2）2=4．

把ρ2=x2+y2，y=ρsinθ，可得C的极坐标方程为：ρ=4sinθ

（2）解：P（1，0）．把直线l的参数方程代入圆C的方程为： +1=0，

t1+t2=3 ，t1t2=1，

∴|PM||PN|=|t1t2|=1．

【解析】（1）直线l的参数方程为 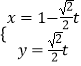（t为参数），消去参数t可得普通方程．曲线C的参数方程为 （θ为参数），利用平方关系可得直角坐标方程．把ρ2=x2+y2 ， y=ρsinθ，可得C的极坐标方程．（II）P（1，0）．把直线l的参数方程代入圆C的方程为： +1=0，|PM||PN|=|t1t2|．