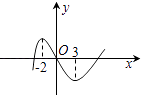题目内容
【题目】给出下列五个命题:
①函数 ![]() 的一条对称轴是x=
的一条对称轴是x= ![]() ;
;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数;
④若 ![]() ,则x1﹣x2=kπ,其中k∈Z;
,则x1﹣x2=kπ,其中k∈Z;
⑤函数f(x)=sinx+2|sinx|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
以上五个命题中正确的有(填写所有正确命题的序号)
【答案】①②
【解析】解:当x= ![]() 时,sin(2x﹣
时,sin(2x﹣ ![]() )=sin
)=sin ![]() =1,∴①正确;
=1,∴①正确;
当x= ![]() 时,tanx无意义,∴②正确;
时,tanx无意义,∴②正确;
当x>0时,y=sinx的图象为“波浪形“曲线,故③错误;
若 ![]() ,则2x1﹣
,则2x1﹣ ![]() =2x2﹣
=2x2﹣ ![]() +2kπ或2x1﹣
+2kπ或2x1﹣ ![]() +(2x2﹣
+(2x2﹣ ![]() )=2(
)=2( ![]() )=π+2kπ,
)=π+2kπ,
∴x1﹣x2=kπ或x1+x2= ![]() +kπ,k∈Z.故④错误.
+kπ,k∈Z.故④错误.
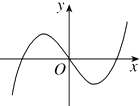
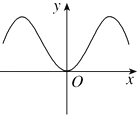
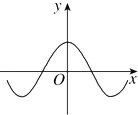
作出f(x)=sinx+2|sinx|在[0,2π]上的函数图象,如图所示:
则f(x)在[0,π]上过原点得切线为y=3x,设f(x)在[π,2π]上过原点得切线为y=k1x,
有图象可知当k1<k<3时,直线y=kx与f(x)有2个不同交点,
∵y=sinx在[0,π]上过原点得切线为y=x,∴k1<1,故⑤不正确.
故答案为:①②.

把x的值带入函数得y=1,为最大值故①正确,由正切函数的图象特征可得![]() 是函数y=tanx的对称中心,故②正确,根据正弦函数的图象可知③不正确, s i n ( 2 x 1
是函数y=tanx的对称中心,故②正确,根据正弦函数的图象可知③不正确, s i n ( 2 x 1 ![]() ) = s i n ( 2 x 2
) = s i n ( 2 x 2 ![]() )得2 x 1
)得2 x 1 ![]() 和 2 x 2
和 2 x 2 ![]() 关于对称轴对称或相差周期的整数倍,⑤作出函数图象,借助图像判断.
关于对称轴对称或相差周期的整数倍,⑤作出函数图象,借助图像判断.

【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
【题目】某媒体对“男女同龄退休”这一公众关注的问题进行 了民意调査,右表是在某单位得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
附表:
P(K2≥K) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
(1 )能否有90%以上的把握认为对这一问题的看法与性别有关?
【答案】解:解:K2= ![]() ≈2.932>2.706,
≈2.932>2.706,
由此可知,有90%的把握认为对这一问题的看法与性别有关
(1)进一步调查:(ⅰ)从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率; (ⅱ)从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和期望.