题目内容
设双曲线方程为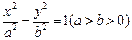
，P为双曲线上任意一点，F为双曲线的一个焦点，讨论以|PF|为直径的圆与圆x2＋y2=a2的位置关系．
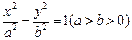，P为双曲线上任意一点，F为双曲线的一个焦点，讨论以|PF|为直径的圆与圆x2＋y2=a2的位置关系．当点P在双曲线的右支上时，外切；当点P在双曲线的左支上时，内切
提示：用双曲线的定义及两圆相切时的几何性质．
练习册系列答案
相关题目
题目内容
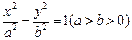，P为双曲线上任意一点，F为双曲线的一个焦点，讨论以|PF|为直径的圆与圆x2＋y2=a2的位置关系．
上动点
到定点
,其中
的距离
的最小值为1.（1）请确定M点的坐标（2）试问是否存在经过M点的直线
,使
（O为原点）,若存在,求出
，b＝xi＋(y－2)j，且|a|＋|b|＝8．
是否存在这样的直线l，使得四边形OAPB为矩形？若存在，求出直线l的方程；若不存在，试说明理由．
在椭圆
上，
直线
与直线
垂直，O为坐标原点，直线OP的倾斜角为
，直线
.
是椭圆
与直线
的唯一交点； 
构成等比数列.
、
分别是椭圆
的左、右焦点.
是该椭圆上的一个动点，求
·
的最大值和最小值;
的直线
与椭圆交于不同的两点
、
，且∠
为锐角（其中
为坐标原点），求直线
的取值范围.
发出的光线沿平行于抛物线
的轴的方向射向此抛物线上的点P，反射后经焦点F又射向抛物线上的点Q，再反射后沿平行于抛物线的轴的方向射向直线
再反射后又射回点M，则 x0= ．
，其焦点F（c，0）（c＞0）对应的准线l与x轴交于A点，|OF|=2|FA|，过A的直线与椭圆交于P、Q两点.
，求直线PQ的方程； （3）设
，过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.