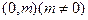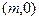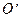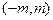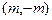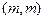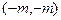题目内容
设x，y∈R，i，j为直角坐标平面内x，y轴正方向上的单位向量，若向量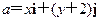
，b＝xi＋(y－2)j，且|a|＋|b|＝8．
（1）求点M（x，y）的轨迹C的方程；
（2）过点（0，3）作直线l与曲线C交于A、B两点，设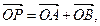
是否存在这样的直线l，使得四边形OAPB为矩形？若存在，求出直线l的方程；若不存在，试说明理由．
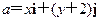，b＝xi＋(y－2)j，且|a|＋|b|＝8．（1）求点M（x，y）的轨迹C的方程；
（2）过点（0，3）作直线l与曲线C交于A、B两点，设
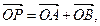是否存在这样的直线l，使得四边形OAPB为矩形？若存在，求出直线l的方程；若不存在，试说明理由．见解析
解：（1）∵a＝xi＋(y＋2)j，b＝xi＋(y－2)j，且|a|＋|b|＝8 ∴点M（x，y）到两个定点F1（0，－2），F2（0，2）的距离之和为8 ∴点M的轨迹C为F1、F2为焦点的椭圆，其方程为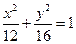
（2）∵l过y轴上的点（0，3），若直线l是y轴，则A、B两点是椭圆的顶点，这时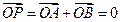
。
∴P与O重合，与四边形OAPB是矩形矛盾，
∴直线l的斜率存在，设l的方程为y＝kx＋3，A（x1，y1），B(x2，y2)
由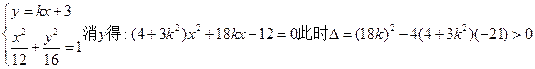
恒成立．
且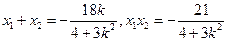
∵
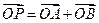，∴四边形OAPB是平行四边形
若存在直线l使得四边形OAPB是矩形，则OA⊥OB，即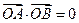
∵
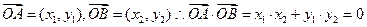
即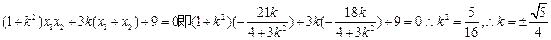
∴存在直线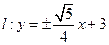
使得四边形OAPB为矩形．
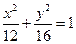
（2）∵l过y轴上的点（0，3），若直线l是y轴，则A、B两点是椭圆的顶点，这时
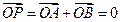。∴P与O重合，与四边形OAPB是矩形矛盾，
∴直线l的斜率存在，设l的方程为y＝kx＋3，A（x1，y1），B(x2，y2)
由
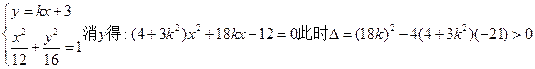恒成立．且
∵
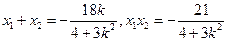
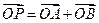，∴四边形OAPB是平行四边形若存在直线l使得四边形OAPB是矩形，则OA⊥OB，即
∵
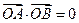
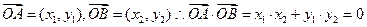
即
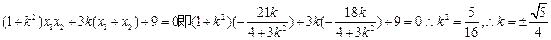∴存在直线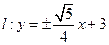使得四边形OAPB为矩形．
练习册系列答案
相关题目
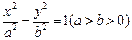，P为双曲线上任意一点，F为双曲线的一个焦点，讨论以|PF|为直径的圆与圆x2＋y2=a2的位置关系．
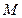与点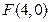
的距离比它到直线
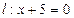的距离小1，求点
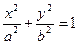(a＞b＞0)，曲线C2的方程为y=
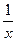，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
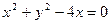外切，且与y轴相切的动圆圆心的轨迹方程为 .
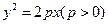焦点F的直线与抛物线的交点，O是坐标原点，满足
，
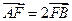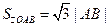，则
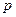的值为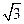 
,若它的一条准线与抛物线
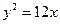的准线重合,则该双曲线的方程是( ) 
