题目内容
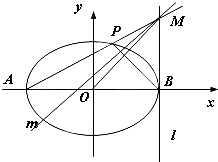
(本小题满分13分)已知椭圆的中心在原点O,短轴长为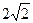 ,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.
,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.
(1)求椭圆的方程;(2)若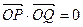 ,求直线PQ的方程; (3)设
,求直线PQ的方程; (3)设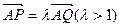 ,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
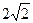 ,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.
,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.(1)求椭圆的方程;(2)若
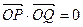 ,求直线PQ的方程; (3)设
,求直线PQ的方程; (3)设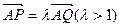 ,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.(1) (2)
(2)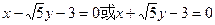
 (2)
(2)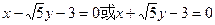
(1)由题意,设椭圆的方程为: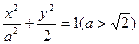
由已知得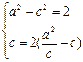 ,解得
,解得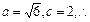 椭圆的方程为:
椭圆的方程为:
(2)由(1)可得,准线l的方程为:
设直线PQ的方程为: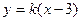
由方程组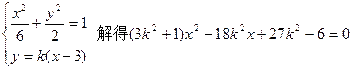
依题意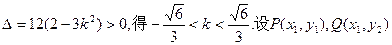 ,则
,则
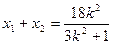 ①
① 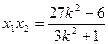 ②
②
由直线PQ的方程得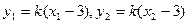 ,
,
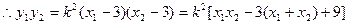 ③
③
又 ④
④
由①②③④得 ,直线PQ的方程为
,直线PQ的方程为
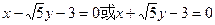 ………………8分
………………8分
(3)证明: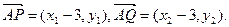
由题意可得方程组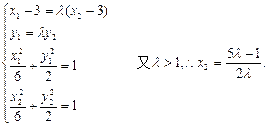
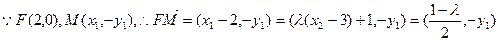
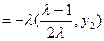
而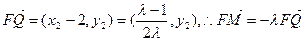
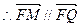 ,又∵直线FM、直线FQ有公共点F 故F、M、Q三点共线.
,又∵直线FM、直线FQ有公共点F 故F、M、Q三点共线.
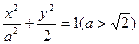
由已知得
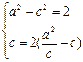 ,解得
,解得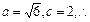 椭圆的方程为:
椭圆的方程为:
(2)由(1)可得,准线l的方程为:

设直线PQ的方程为:
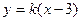
由方程组
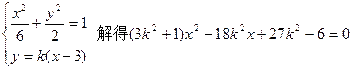
依题意
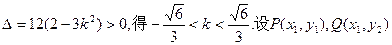 ,则
,则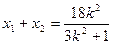 ①
① 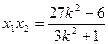 ②
② 由直线PQ的方程得
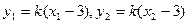 ,
,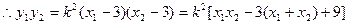 ③
③又
 ④
④ 由①②③④得
 ,直线PQ的方程为
,直线PQ的方程为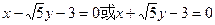 ………………8分
………………8分(3)证明:
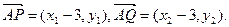
由题意可得方程组
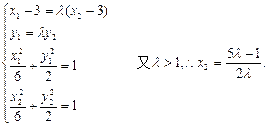
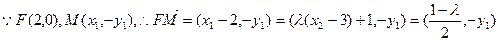
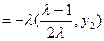
而
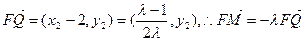
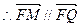 ,又∵直线FM、直线FQ有公共点F 故F、M、Q三点共线.
,又∵直线FM、直线FQ有公共点F 故F、M、Q三点共线. 
练习册系列答案
相关题目
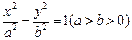 ,P为双曲线上任意一点,F为双曲线的一个焦点,讨论以|PF|为直径的圆与圆x2+y2=a2的位置关系.
,P为双曲线上任意一点,F为双曲线的一个焦点,讨论以|PF|为直径的圆与圆x2+y2=a2的位置关系.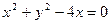 外切,且与y轴相切的动圆圆心的轨迹方程为 .
外切,且与y轴相切的动圆圆心的轨迹方程为 .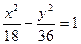 的顶点都是椭圆
的顶点都是椭圆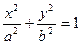 的顶点,直线
的顶点,直线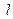 :
: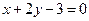 经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线
经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线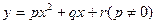 经过椭圆的两个焦点,与直线
经过椭圆的两个焦点,与直线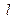 相交于
相交于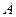 、
、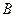 ,试将线段
,试将线段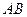 的长
的长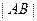 表示为
表示为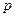 的函数.
的函数.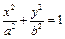 (a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且
(a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且 最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.
最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.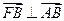 时,其离心率为
时,其离心率为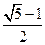 ,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲
,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲ 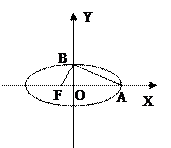
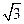 ,若它的一条准线与抛物线
,若它的一条准线与抛物线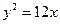 的准线重合,则该双曲线的方程是( )
的准线重合,则该双曲线的方程是( )