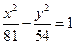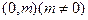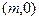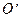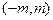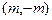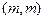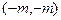题目内容
已知椭圆C:
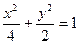 上动点
上动点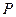 到定点
到定点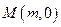 ,其中
,其中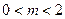 的距离
的距离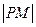 的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线
的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线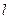 ,使
,使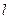 与椭圆C的两个交点A、B满足条件
与椭圆C的两个交点A、B满足条件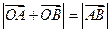 (O为原点),若存在,求出
(O为原点),若存在,求出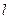 的方程,若不存在请说是理由。
的方程,若不存在请说是理由。(1,0);这样的直线不存在。
【思维分析】此题解题关键是由条件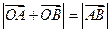 知
知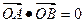 从而将条件转化点的坐标运算再结合韦达定理解答。
从而将条件转化点的坐标运算再结合韦达定理解答。
解析:设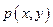 ,由
,由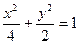 得
得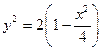 故
故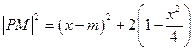
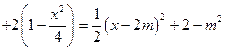 由于
由于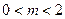 且
且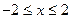 故当
故当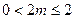 时,
时,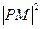 的最小值为
的最小值为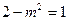 此时
此时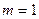 ,当
,当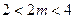 时,
时,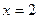 取得最小值为
取得最小值为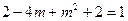 解得
解得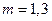 不合题意舍去。综上所知当
不合题意舍去。综上所知当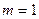 是满足题意此时M的坐标为(1,0)。
是满足题意此时M的坐标为(1,0)。
(2)由题意知条件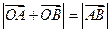 等价于
等价于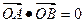 ,当
,当 的斜率不存在时,
的斜率不存在时, 与C的交点为
与C的交点为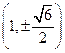 ,此时
,此时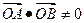 ,设
,设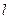 的方程为
的方程为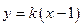 ,代入椭圆方程整理得
,代入椭圆方程整理得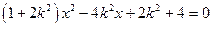 ,由于点M在椭圆内部故
,由于点M在椭圆内部故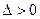 恒成立,由
恒成立,由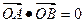 知
知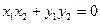 即
即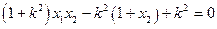 ,据韦达定理得
,据韦达定理得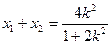 ,
,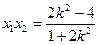 代入上式得
代入上式得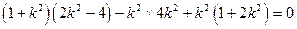 得
得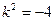 不合题意。综上知这样的直线不存在。
不合题意。综上知这样的直线不存在。
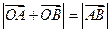 知
知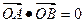 从而将条件转化点的坐标运算再结合韦达定理解答。
从而将条件转化点的坐标运算再结合韦达定理解答。解析:设
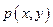 ,由
,由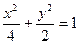 得
得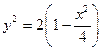 故
故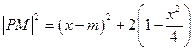
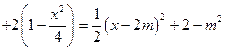 由于
由于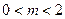 且
且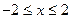 故当
故当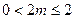 时,
时,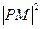 的最小值为
的最小值为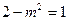 此时
此时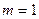 ,当
,当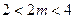 时,
时,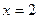 取得最小值为
取得最小值为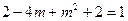 解得
解得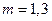 不合题意舍去。综上所知当
不合题意舍去。综上所知当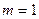 是满足题意此时M的坐标为(1,0)。
是满足题意此时M的坐标为(1,0)。(2)由题意知条件
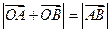 等价于
等价于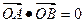 ,当
,当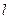 的斜率不存在时,
的斜率不存在时, 与C的交点为
与C的交点为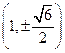 ,此时
,此时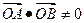 ,设
,设 的方程为
的方程为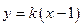 ,代入椭圆方程整理得
,代入椭圆方程整理得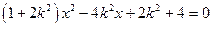 ,由于点M在椭圆内部故
,由于点M在椭圆内部故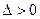 恒成立,由
恒成立,由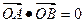 知
知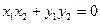 即
即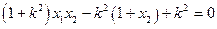 ,据韦达定理得
,据韦达定理得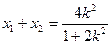 ,
,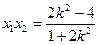 代入上式得
代入上式得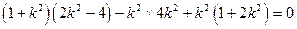 得
得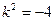 不合题意。综上知这样的直线不存在。
不合题意。综上知这样的直线不存在。【知识点归类点拔】在解题过程中要注意将在向量给出的条件转化向量的坐标运算,从而与两交点的坐标联系起来才自然应用韦达定理建立起关系式。此题解答具有很强的示范性,请同学们认真体会、融会贯通。

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
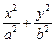 =1(a>b>0)与直线l: x+y=1在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域.
=1(a>b>0)与直线l: x+y=1在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域. 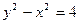
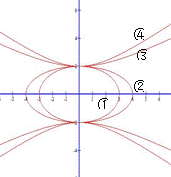 为
为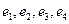 ,其大小关系为 ( )
,其大小关系为 ( )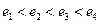
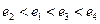
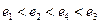
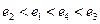
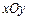 中,
中,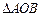 和
和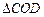 为两等腰直角三角形,
为两等腰直角三角形,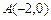 ,C(a,0)(a>0).设
,C(a,0)(a>0).设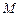 ,
,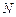 .
.
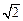 ,若存在,求此时⊙N的标准方程;若不存在,说明理由.
,若存在,求此时⊙N的标准方程;若不存在,说明理由.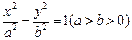 ,P为双曲线上任意一点,F为双曲线的一个焦点,讨论以|PF|为直径的圆与圆x2+y2=a2的位置关系.
,P为双曲线上任意一点,F为双曲线的一个焦点,讨论以|PF|为直径的圆与圆x2+y2=a2的位置关系.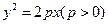 焦点F的直线与抛物线的交点,O是坐标原点,满足
焦点F的直线与抛物线的交点,O是坐标原点,满足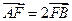 ,
,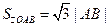 ,则
,则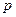 的值为
的值为 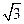 ,若它的一条准线与抛物线
,若它的一条准线与抛物线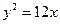 的准线重合,则该双曲线的方程是( )
的准线重合,则该双曲线的方程是( )