题目内容
如图,在直四棱柱ABCD-A1B1C 1D1中,底面ABCD是梯形BC∥AD,∠DAB=90°,AB=BB1=4,BC=3,AD=5,AE=3,F、G分别为CD、C1D1的中点.
1D1中,底面ABCD是梯形BC∥AD,∠DAB=90°,AB=BB1=4,BC=3,AD=5,AE=3,F、G分别为CD、C1D1的中点.
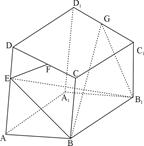
(1)求证:EF⊥平面BB1G;
(2)求二面角E-BB1-G的大小.
 1D1中,底面ABCD是梯形BC∥AD,∠DAB=90°,AB=BB1=4,BC=3,AD=5,AE=3,F、G分别为CD、C1D1的中点.
1D1中,底面ABCD是梯形BC∥AD,∠DAB=90°,AB=BB1=4,BC=3,AD=5,AE=3,F、G分别为CD、C1D1的中点.
(1)求证:EF⊥平面BB1G;
(2)求二面角E-BB1-G的大小.
(1)略
(2)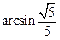
(2)
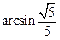
(1)
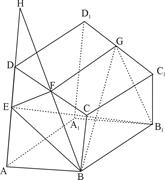
连接FG ∵F、G分别为CD、C1D1的中点,
∴FG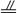 CC1 从而FG
CC1 从而FG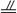 BB1
BB1
∴B、B1、F、G四点共面.
连接BF并延长与AD的延长线交于点H.
∵F为CD的中点,且BC∥A D.
∴△HFD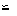 △BFC ∴DH=BC=3
△BFC ∴DH=BC=3
∴EH=DE+DH=5. 又∵BE=5,且F为BH的中点.
∴EF⊥BF,又∵BB1⊥平面ABCD,且EF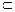 平面ABCD内.
平面ABCD内.
∴BB1⊥EF ∴EF⊥平面BB1GF. 从而EF⊥平面BB1G.
(2)二面角E-BB1-G的大小等于二面角F-BB1-E的大小
∵EF⊥平面FBB1 且EB⊥BB1 FB⊥BB1
即∠EBF为二面角F-BB1-E的平面角
在△EFB中,EB=5,EF=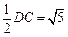 . ∴
. ∴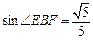
∴∠EBF=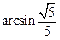 ∴二面角E-BB1-G的大小为
∴二面角E-BB1-G的大小为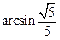
解法2:以A为坐标原点,AB为x轴,AA1为y轴,AD为Z轴建立空间直角坐标系,
则E(0,0,3)、F(2,0,4)、G(2,4,4)、B(4,0,0)、B1(4,4,0)
(1)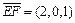 、
、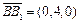 、
、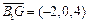
∵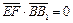 ,
,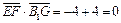
∴EF⊥BB1,EF⊥B1G ∴EF⊥平面BB1G
(2)∵EF⊥平面BB1G ∴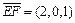 为平面BB1G的一个法向量
为平面BB1G的一个法向量
设平面EBB1的一个 法向量为
法向量为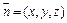
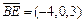
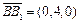
则 解得
解得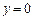 ,取
,取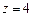
∴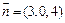
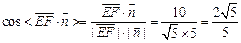
∴二面角E-BB1-G的大小为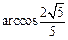

连接FG ∵F、G分别为CD、C1D1的中点,
∴FG
 CC1 从而FG
CC1 从而FG BB1
BB1∴B、B1、F、G四点共面.
连接BF并延长与AD的延长线交于点H.
∵F为CD的中点,且BC∥A D.
∴△HFD
 △BFC ∴DH=BC=3
△BFC ∴DH=BC=3∴EH=DE+DH=5. 又∵BE=5,且F为BH的中点.
∴EF⊥BF,又∵BB1⊥平面ABCD,且EF
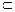 平面ABCD内.
平面ABCD内.∴BB1⊥EF ∴EF⊥平面BB1GF. 从而EF⊥平面BB1G.
(2)二面角E-BB1-G的大小等于二面角F-BB1-E的大小
∵EF⊥平面FBB1 且EB⊥BB1 FB⊥BB1
即∠EBF为二面角F-BB1-E的平面角
在△EFB中,EB=5,EF=
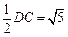 . ∴
. ∴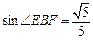
∴∠EBF=
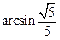 ∴二面角E-BB1-G的大小为
∴二面角E-BB1-G的大小为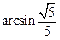
解法2:以A为坐标原点,AB为x轴,AA1为y轴,AD为Z轴建立空间直角坐标系,
则E(0,0,3)、F(2,0,4)、G(2,4,4)、B(4,0,0)、B1(4,4,0)
(1)
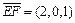 、
、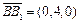 、
、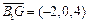
∵
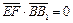 ,
,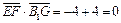
∴EF⊥BB1,EF⊥B1G ∴EF⊥平面BB1G
(2)∵EF⊥平面BB1G ∴
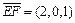 为平面BB1G的一个法向量
为平面BB1G的一个法向量设平面EBB1的一个
 法向量为
法向量为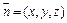
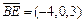
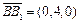
则
 解得
解得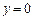 ,取
,取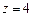
∴
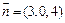
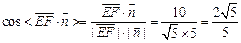
∴二面角E-BB1-G的大小为
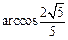

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
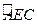 是半径为
是半径为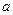 的半圆,
的半圆,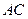 为直径,点
为直径,点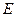 为
为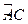 的中点,点
的中点,点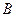 和点
和点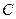 为线段
为线段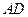 的三等分点,平面
的三等分点,平面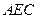 外一点
外一点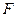 满足
满足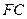
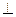 平面
平面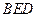 ,
,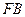 =
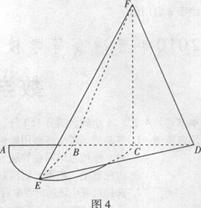
=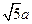 .
. 
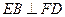 ;
; 的距离.
的距离.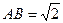 ,
,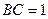 ,现沿对角线
,现沿对角线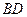 折成二面角
折成二面角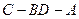 ,使
,使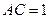 (如图).
(如图).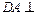 面
面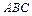 ;
; 平面角的大小.
平面角的大小.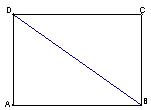

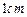 的正方体。
的正方体。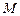 、
、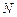 、
、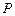 、
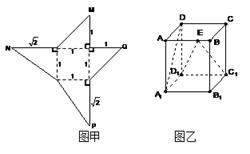
、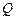 重合,则可以围成怎样的几何体?请求出此几何体的体积;
重合,则可以围成怎样的几何体?请求出此几何体的体积; 体?请按图乙中所标字母写出这几个几何体的名称;
体?请按图乙中所标字母写出这几个几何体的名称;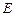 为棱
为棱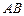 上的动点,试判断
上的动点,试判断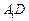 与平面
与平面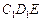 是否垂直,并说明理由。
是否垂直,并说明理由。
 中,
中,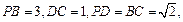
 为
为 边上一点,
边上一点,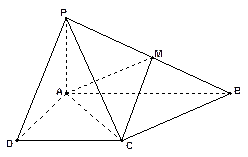
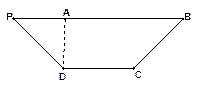
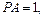 将
将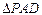 沿
沿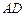 折起,使平面
折起,使平面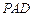 ⊥平面
⊥平面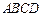 .
.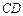 ⊥平面
⊥平面 是侧棱
是侧棱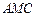 把几何体分成的两部分的体积之比。
把几何体分成的两部分的体积之比。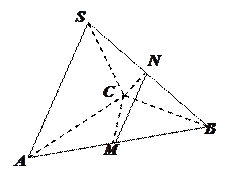 在三棱锥
在三棱锥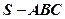 中,
中,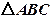 是边长为
是边长为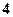 的正三角形,平面
的正三角形,平面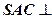 平面
平面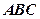 ,
,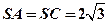 ,
,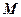 、
、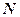 分别为
分别为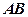 、
、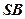 的中点,
的中点,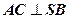 ;
;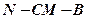 的大小;
的大小;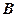 到平面
到平面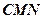 的距离.
的距离.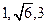 ,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。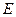 在棱
在棱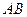 上,
上,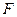 在棱
在棱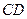 上.并且
上.并且 (0<l<+∞),设a为异面直线
(0<l<+∞),设a为异面直线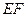 与
与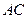 所成的角,b 为异面直线EF与BD所成的角,则a+b的值是
所成的角,b 为异面直线EF与BD所成的角,则a+b的值是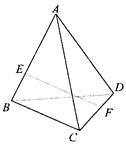
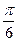
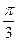
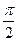
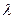 的值有关
的值有关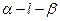 的大小为
的大小为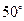 ,
,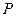 为空间中任意一点,则过点
为空间中任意一点,则过点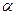 和平面
和平面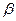 所成的角都是
所成的角都是 的直线的条数为( )
的直线的条数为( )