题目内容
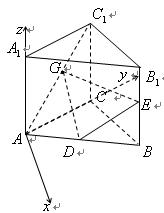
(本小题满分12分)如图,在正三棱柱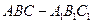 中,
中,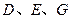 分别是
分别是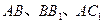 的中点,
的中点,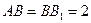 .
.
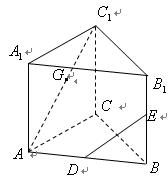
(Ⅰ)在棱 上是否存在点
上是否存在点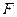 使
使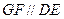 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;
(Ⅱ)求截面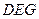 与底面
与底面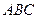 所成锐二面角的正切值;
所成锐二面角的正切值;
(Ⅲ)求点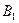 到截面
到截面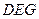 的距离.
的距离.
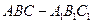 中,
中,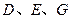 分别是
分别是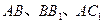 的中点,
的中点,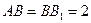 .
.
(Ⅰ)在棱
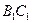 上是否存在点
上是否存在点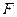 使
使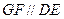 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;(Ⅱ)求截面
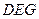 与底面
与底面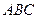 所成锐二面角的正切值;
所成锐二面角的正切值;(Ⅲ)求点
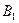 到截面
到截面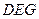 的距离.
的距离.(Ⅰ)存在且为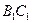 的中点
的中点
(Ⅱ)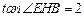
(Ⅲ)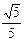
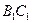 的中点
的中点(Ⅱ)
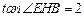
(Ⅲ)
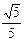
解法一:(Ⅰ)存在且为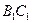 的中点,连接
的中点,连接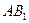 ,
,
∵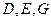 分别是
分别是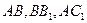 的中点, ∴
的中点, ∴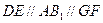 . (3分)
. (3分)
(Ⅱ)延长 与
与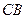 的延长线交于
的延长线交于 ,连接
,连接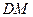 ,
,
则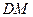 为截面与底面所成二面角的棱,
为截面与底面所成二面角的棱,
取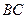 的中点
的中点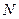 ,连
,连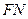 ,则
,则 .
.

∵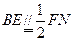 ,∴
,∴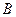 为
为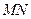 的中点.
的中点.
由题设得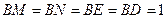 ,且
,且 ,
,
作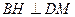 于
于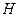 ,则
,则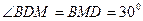 ,连
,连 ,
,
又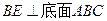 ,
,
由三垂线定理可知 ,
,
∴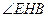 为截面与底面所成的锐二面角. (6分)
为截面与底面所成的锐二面角. (6分)
在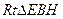 中,
中,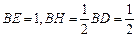 ,∴
,∴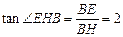 .
.  (8分)
(8分)
(Ⅲ)在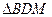 中,得
中,得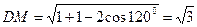 ,
,
在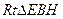 中,得
中,得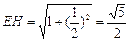 ,
,
由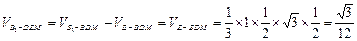 ,
,
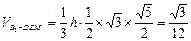 ,解得
,解得 ,即
,即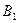 到截面距离为
到截面距离为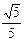 . (12分)
. (12分)
解法二:(Ⅱ)如图,以 为坐标原点,
为坐标原点,
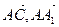 的方向分别
的方向分别 作为
作为 轴的正方向建立空间直角坐标系,
轴的正方向建立空间直角坐标系,
则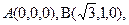
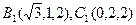 ;
;
∵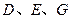 分别是
分别是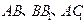
的中点,∴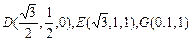 ,
,
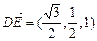 ,
,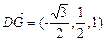 ;
;
设平 面
面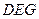 的法向量为
的法向量为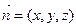 ,
,
由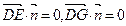 得
得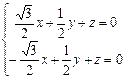 ,
,
解得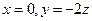 ,取
,取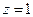 得
得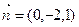 ;
;
又平面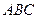 的一个法向量为
的一个法向量为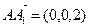 , (6分)
, (6分)
设截面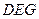 与底面
与底面 所成锐二面角为
所成锐二面角为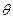
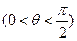 ,
,
则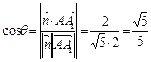 ,
,
∴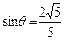 ,得
,得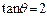 .
.
故截面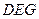 与底
与底 面
面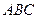 所成锐二面角的正切值为2. (8分)
所成锐二面角的正切值为2. (8分)
(Ⅲ)由(Ⅱ)知平面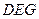 的一个法向量为
的一个法向量为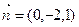 ,
,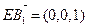 ;
;
设点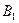 到截面
到截面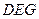 的距离为
的距离为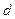 ,
,
由向量的投影得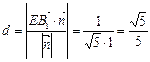 ,
,
故点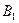 到截面
到截面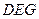 的距离为
的距离为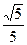 . (12分)
. (12分)
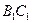 的中点,连接
的中点,连接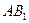 ,
,∵
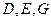 分别是
分别是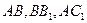 的中点, ∴
的中点, ∴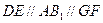 . (3分)
. (3分)(Ⅱ)延长
 与
与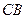 的延长线交于
的延长线交于 ,连接
,连接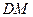 ,
,则
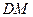 为截面与底面所成二面角的棱,
为截面与底面所成二面角的棱,取
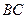 的中点
的中点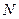 ,连
,连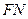 ,则
,则 .
.
∵
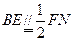 ,∴
,∴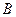 为
为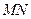 的中点.
的中点.由题设得
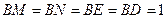 ,且
,且 ,
,作
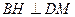 于
于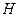 ,则
,则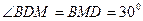 ,连
,连 ,
,又
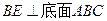 ,
,由三垂线定理可知
 ,
,∴
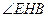 为截面与底面所成的锐二面角. (6分)
为截面与底面所成的锐二面角. (6分)在
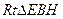 中,
中,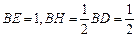 ,∴
,∴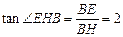 .
.  (8分)
(8分)(Ⅲ)在
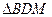 中,得
中,得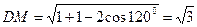 ,
,在
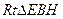 中,得
中,得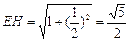 ,
,由
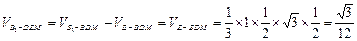 ,
,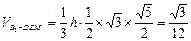 ,解得
,解得 ,即
,即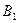 到截面距离为
到截面距离为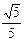 . (12分)
. (12分)解法二:(Ⅱ)如图,以
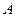 为坐标原点,
为坐标原点,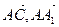 的方向分别
的方向分别 作为
作为 轴的正方向建立空间直角坐标系,
轴的正方向建立空间直角坐标系,
则
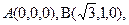
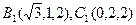 ;
;∵
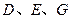 分别是
分别是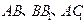
的中点,∴
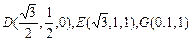 ,
,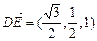 ,
,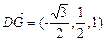 ;
;设平
 面
面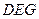 的法向量为
的法向量为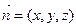 ,
,由
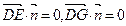 得
得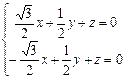 ,
,解得
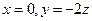 ,取
,取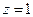 得
得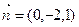 ;
;又平面
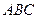 的一个法向量为
的一个法向量为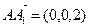 , (6分)
, (6分)设截面
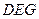 与底面
与底面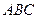 所成锐二面角为
所成锐二面角为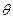
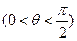 ,
,则
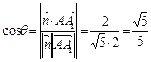 ,
,∴
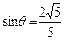 ,得
,得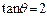 .
.故截面
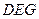 与底
与底 面
面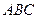 所成锐二面角的正切值为2. (8分)
所成锐二面角的正切值为2. (8分)(Ⅲ)由(Ⅱ)知平面
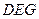 的一个法向量为
的一个法向量为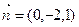 ,
,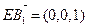 ;
;设点
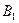 到截面
到截面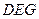 的距离为
的距离为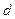 ,
,由向量的投影得
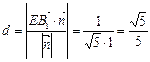 ,
,故点
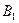 到截面
到截面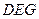 的距离为
的距离为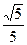 . (12分)
. (12分)
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
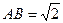 ,
,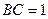 ,现沿对角线
,现沿对角线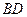 折成二面角
折成二面角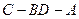 ,使
,使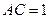 (如图).
(如图).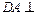 面
面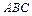 ;
;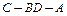 平面角的大小.
平面角的大小.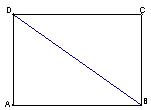

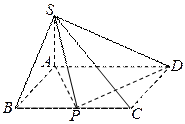 如图,四棱锥
如图,四棱锥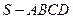 的底面是矩形,
的底面是矩形,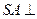 底面
底面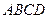 ,P为BC边的中点,SB与
,P为BC边的中点,SB与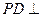 平面SAP;
平面SAP;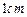 的正方体。
的正方体。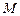 、
、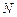 、
、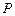 、
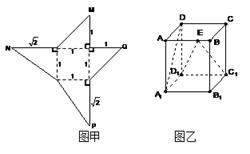
、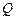 重合,则可以围成怎样的几何体?请求出此几何体的体积;
重合,则可以围成怎样的几何体?请求出此几何体的体积; 体?请按图乙中所标字母写出这几个几何体的名称;
体?请按图乙中所标字母写出这几个几何体的名称;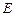 为棱
为棱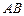 上的动点,试判断
上的动点,试判断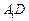 与平面
与平面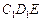 是否垂直,并说明理由。
是否垂直,并说明理由。
 在三棱锥
在三棱锥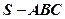 中,
中,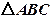 是边长为
是边长为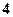 的正三角形,平面
的正三角形,平面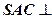 平面
平面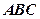 ,
,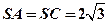 ,
,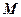 、
、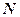 分别为
分别为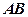 、
、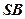 的中点,
的中点,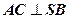 ;
;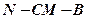 的大小;
的大小;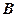 到平面
到平面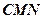 的距离.
的距离.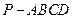 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.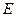 是侧棱
是侧棱 上的动点.
上的动点.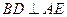
 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
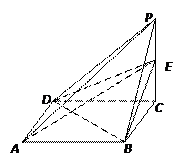
 中,
中,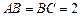 ,过
,过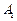 、
、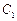 、
、 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体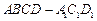 ,且这个几何体的体积为
,且这个几何体的体积为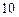 .
.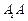 的长;
的长;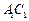 的中点为
的中点为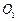 ,求异面直线
,求异面直线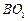 与
与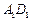 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).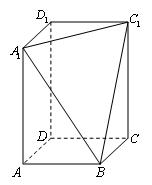
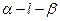 的大小为
的大小为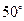 ,
,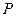 为空间中任意一点,则过点
为空间中任意一点,则过点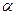 和平面
和平面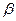 所成的角都是
所成的角都是 的直线的条数为( )
的直线的条数为( )
 --
--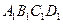 ,E、F分别是
,E、F分别是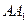 、
、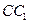 的中点,p是
的中点,p是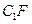 B、线段
B、线段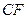 C、线段
C、线段 D、线段
D、线段