题目内容
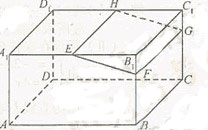
(本题12分)如图,四棱柱ABCD—A B
B C
C D
D 中,A
中,A D
D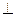 平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
平面ABCD,底面ABCD是边长为1的正方形,侧棱AA =2.
=2.
(1)求证:C D∥平面ABB
D∥平面ABB A
A ;
;
(2)求直线BD 与平面A
与平面A C
C D所成角的正弦值;
D所成角的正弦值;
(3)求二面角D—A C
C 一A的余弦值.
一A的余弦值.
 B
B C
C D
D 中,A
中,A D
D 平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
平面ABCD,底面ABCD是边长为1的正方形,侧棱AA =2.
=2.(1)求证:C
 D∥平面ABB
D∥平面ABB A
A ;
;(2)求直线BD
 与平面A
与平面A C
C D所成角的正弦值;
D所成角的正弦值;(3)求二面角D—A
 C
C 一A的余弦值.
一A的余弦值.
(1)证明见解析。
(2)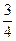
(3)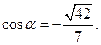
(2)
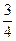
(3)
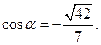
(1)证明:四棱柱ABCD—A1B1C1D1中,BB1//CC1,
又CC1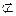 面ABB1A1,
面ABB1A1, 所以CC1//平面ABB1A1,
所以CC1//平面ABB1A1,
ABCD是正方形,所以CD//AB,
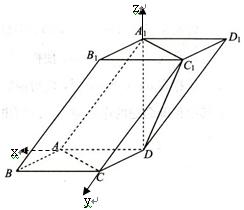
又CD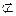 面ABB1A1,所以CD//平面ABB1A1,
面ABB1A1,所以CD//平面ABB1A1,
所以平面CDD1C1//平面ABB1A1,
所以C1D//平面ABB1A1。
(2)ABCD是正方形,AD⊥CD,
因为A1D⊥平面ABCD,所以A1D⊥AD,A1D⊥CD,
如图,以D为原点建立空间直角坐标系D-xyz,
在△ADA1中,由已知可得A1D=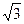 ,
,
所以D(0,0,0),A1(0,0,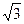 ),A(1,0,0),C1(-1,1,
),A(1,0,0),C1(-1,1,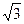 )
)
B1(0,1,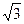 ),D1(-1,0,
),D1(-1,0,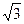 ),B(0,1,0)
),B(0,1,0)
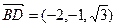
因为A1D⊥平面ABCD,
所以A1D⊥平面A1B1C1D1,
A1D⊥B1D1,
又B1D1⊥A1C1,
所以B1D1⊥平面A1C1D1,
所以平面A1C1D1的一个法向量为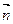 =(1,1,0)
=(1,1,0)
设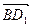 与
与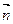 所成的角为β,
所成的角为β,
则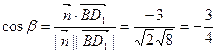 ,
,
所以直线BD1与平面A1C1D1所成角的正弦值为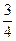 。
。
(3)设平面A1C1A的法向量为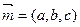 ,
,
则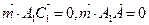 ,所以
,所以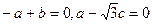
令c=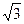 ,可得=
,可得=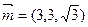
设二面角D—A1C1—A的大小为α,
则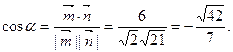
又CC1
 面ABB1A1,
面ABB1A1, 所以CC1//平面ABB1A1,
所以CC1//平面ABB1A1,ABCD是正方形,所以CD//AB,
又CD
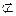 面ABB1A1,所以CD//平面ABB1A1,
面ABB1A1,所以CD//平面ABB1A1,所以平面CDD1C1//平面ABB1A1,
所以C1D//平面ABB1A1。
(2)ABCD是正方形,AD⊥CD,
因为A1D⊥平面ABCD,所以A1D⊥AD,A1D⊥CD,
如图,以D为原点建立空间直角坐标系D-xyz,

在△ADA1中,由已知可得A1D=
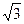 ,
,所以D(0,0,0),A1(0,0,
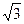 ),A(1,0,0),C1(-1,1,
),A(1,0,0),C1(-1,1,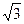 )
)B1(0,1,
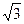 ),D1(-1,0,
),D1(-1,0,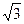 ),B(0,1,0)
),B(0,1,0)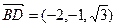
因为A1D⊥平面ABCD,
所以A1D⊥平面A1B1C1D1,
A1D⊥B1D1,
又B1D1⊥A1C1,
所以B1D1⊥平面A1C1D1,
所以平面A1C1D1的一个法向量为
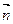 =(1,1,0)
=(1,1,0)设
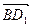 与
与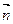 所成的角为β,
所成的角为β,则
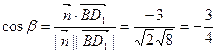 ,
,所以直线BD1与平面A1C1D1所成角的正弦值为
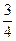 。
。(3)设平面A1C1A的法向量为
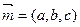 ,
,则
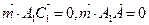 ,所以
,所以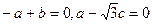
令c=
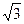 ,可得=
,可得=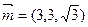
设二面角D—A1C1—A的大小为α,
则
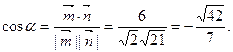

练习册系列答案
相关题目
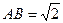 ,
,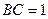 ,现沿对角线
,现沿对角线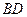 折成二面角
折成二面角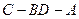 ,使
,使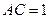 (如图).
(如图).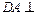 面
面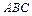 ;
;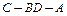 平面角的大小.
平面角的大小.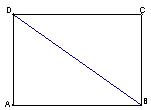

 ,
,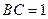 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为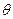 ,且
,且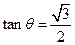 ,
,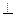 平面ABC.
平面ABC.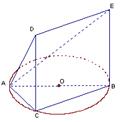
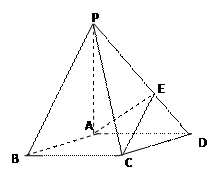 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=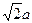 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1. 的大小.
的大小.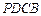 中,
中,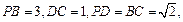
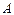 为
为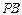 边上一点,
边上一点,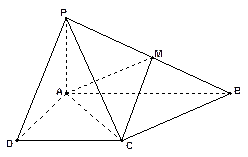
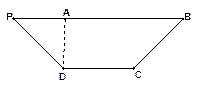
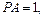 将
将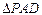 沿
沿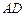 折起,使平面
折起,使平面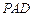 ⊥平面
⊥平面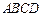 .
.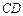 ⊥平面
⊥平面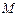 是侧棱
是侧棱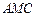 把几何体分成的两部分的体积之比。
把几何体分成的两部分的体积之比。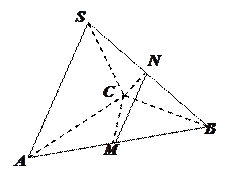 在三棱锥
在三棱锥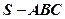 中,
中,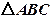 是边长为
是边长为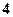 的正三角形,平面
的正三角形,平面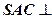 平面
平面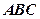 ,
,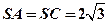 ,
,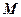 、
、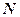 分别为
分别为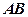 、
、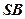 的中点,
的中点,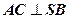 ;
;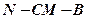 的大小;
的大小;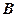 到平面
到平面 的距离.
的距离.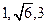 ,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。 --
-- ,E、F分别是
,E、F分别是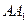 、
、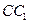 的中点,p是
的中点,p是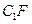 B、线段
B、线段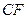 C、线段
C、线段 D、线段
D、线段