题目内容
某圆锥曲线有两个焦点F1、F2,其上存在一点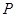 满足
满足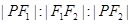 =4:3:2,则此圆锥曲线的离心率等于
=4:3:2,则此圆锥曲线的离心率等于
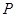 满足
满足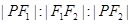 =4:3:2,则此圆锥曲线的离心率等于
=4:3:2,则此圆锥曲线的离心率等于A.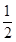 或 或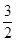 | B.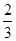 或2 或2 | C.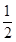 或2 或2 | D.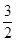 或 或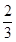 |
A
因为该圆锥曲线有两个交点,所以可能是椭圆或双曲线。因为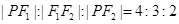 ,所以可设
,所以可设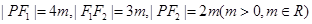 。若该圆锥曲线为椭圆,则有
。若该圆锥曲线为椭圆,则有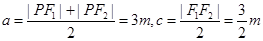 ,此时
,此时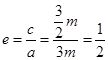 。若该圆锥曲线为双曲线,则有
。若该圆锥曲线为双曲线,则有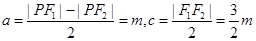 ,此时
,此时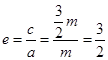 。所以可得圆锥曲线的额离心率为
。所以可得圆锥曲线的额离心率为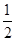 或
或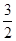 ,故选A
,故选A
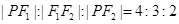 ,所以可设
,所以可设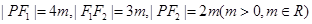 。若该圆锥曲线为椭圆,则有
。若该圆锥曲线为椭圆,则有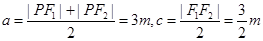 ,此时
,此时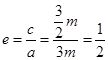 。若该圆锥曲线为双曲线,则有
。若该圆锥曲线为双曲线,则有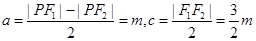 ,此时
,此时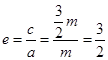 。所以可得圆锥曲线的额离心率为
。所以可得圆锥曲线的额离心率为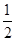 或
或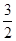 ,故选A
,故选A
练习册系列答案
相关题目
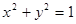 上运动时,它与定点Q(3,0)所连线段PQ的中点M的轨迹方程是:
上运动时,它与定点Q(3,0)所连线段PQ的中点M的轨迹方程是: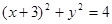
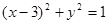
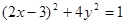
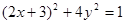
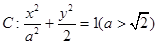 的左右焦点分别为F1,F2,A是椭圆C上第一象限内一点,
的左右焦点分别为F1,F2,A是椭圆C上第一象限内一点,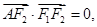 坐标原点O到直线AF1的距离为
坐标原点O到直线AF1的距离为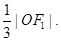
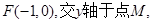 若
若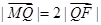 ,求直线l的斜率。
,求直线l的斜率。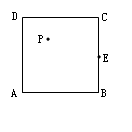
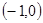 ,B
,B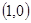 ,动点D,E满足:①
,动点D,E满足:①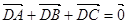 ;②
;②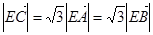 ,③
,③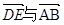 共线.
共线. 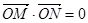 ,若存在,求该圆的方程;若不存在,请说明理由.
,若存在,求该圆的方程;若不存在,请说明理由. 在
在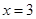 处取得极大值
处取得极大值 .
. 在区间
在区间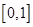 上的最大值;
上的最大值;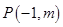 可作曲线
可作曲线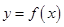 的切线有三条,求实数
的切线有三条,求实数 的取值范围.
的取值范围.
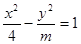 的渐近线方程为
的渐近线方程为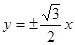 ,则双曲线的焦点坐标是
,则双曲线的焦点坐标是 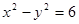 ”是“双曲线离心率
”是“双曲线离心率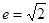 ”的 ( )
”的 ( )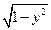 恰有一个交点,则实数的b的取值范围是__________
恰有一个交点,则实数的b的取值范围是__________