题目内容
已知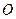 为抛物线
为抛物线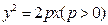 的顶点,
的顶点,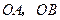 为这条抛物线互相垂直的两条动弦.
为这条抛物线互相垂直的两条动弦.
求证:直线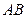 必过一定点.
必过一定点.
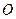 为抛物线
为抛物线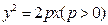 的顶点,
的顶点,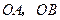 为这条抛物线互相垂直的两条动弦.
为这条抛物线互相垂直的两条动弦.求证:直线
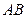 必过一定点.
必过一定点.证明见答案
设 ,
,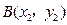 ,则
,则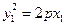 ,
,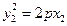 .
.
 ,
,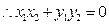 ,可求得
,可求得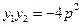 .
.
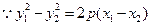 ,
,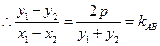 ,
,
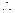 直线
直线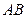 的方程为
的方程为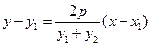 ,
,
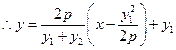 ,
,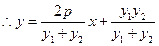 ,
,
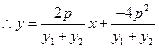 ,
,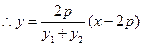 .
.
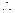 直线
直线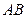 过定点
过定点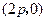 .
.
 ,
,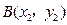 ,则
,则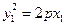 ,
,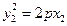 .
. ,
,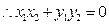 ,可求得
,可求得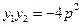 .
.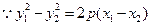 ,
,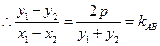 ,
, 直线
直线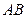 的方程为
的方程为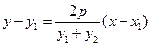 ,
,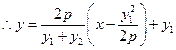 ,
,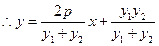 ,
,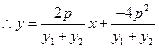 ,
,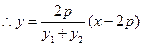 .
.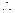 直线
直线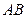 过定点
过定点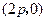 .
.
练习册系列答案
相关题目
题目内容
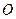 为抛物线
为抛物线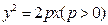 的顶点,
的顶点,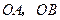 为这条抛物线互相垂直的两条动弦.
为这条抛物线互相垂直的两条动弦.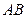 必过一定点.
必过一定点. ,
,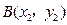 ,则
,则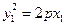 ,
,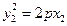 .
. ,
,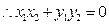 ,可求得
,可求得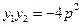 .
.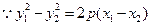 ,
,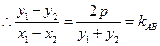 ,
,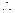 直线
直线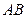 的方程为
的方程为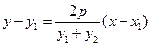 ,
,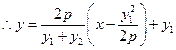 ,
,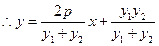 ,
,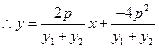 ,
,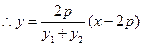 .
. 直线
直线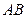 过定点
过定点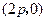 .
.