Question

【题目】如图为函数y=f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）图象的一部分，其中点 是图象的一个最高点，点 是与点P相邻的图象与x轴的一个交点．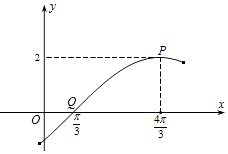

（1）求函数f（x）的解析式；
（2）若将函数f（x）的图象沿x轴向右平移 个单位，再把所得图象上每一点的横坐标都变为原来的 （纵坐标不变），得到函数y=g（x）的图象，求函数y=g（x）的单调递增区间．

Answer 1

【答案】
（1）解：由函数y=f（x）=Asin（ωx+φ）的图象知A=2，

又 ，

∴ ， ；

又∵点 是函数图象y=f（x）的一个最高点，

则 ，

∴ ，

∵|φ|＜π，∴ ，

∴

（2）解：由（1）得， ，

把函数f（x）的图象沿x轴向右平移 个单位，

得到 ，

再把所得图象上每一点的横坐标都变为原来的 （纵坐标不变），

得到 ，

由 ，

解得 ，

∴g（x）的单调增区间是

【解析】（1）由函数y=f（x）的图象求出A、T、ω和φ的值，写出f（x）的解析式，（2）根据函数图象平移法则，得出平移后的函数解析式，求出它的单调递增区间.