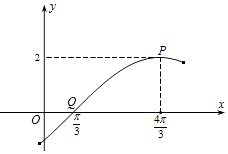题目内容
【题目】已知函数f（x）=ax2+（2a﹣1）x﹣lnx，a∈R．
（1）若曲线y=f（x）在点（1，f（1））处的切线经过点（2，11），求实数a的值；
（2）若函数f（x）在区间（2，3）上单调，求实数a的取值范围；
（3）设 
，若对x1∈（0，+∞），x2∈[0，π]，使得f（x1）+g（x2）≥2成立，求整数a的最小值．
【答案】
（1）解：由题意得， 
，
∴f'（1）=2（2a﹣1），∵f（1）=3a﹣1，
∴曲线y=f（x）在点（1，f（1））处的切线方程为y=2（2a﹣1）（x﹣1）+3a﹣1，
代入点（2，11），得a=2
（2）解：∵ 
，
∴若函数f（x）在区间（2，3）上单调递增，则y=2ax﹣1≥0在（2，3）恒成立，∴ 
，得 
；
若函数f（x）在区间（2，3）上单调递减，则y=2ax﹣1≤0在（2，3）恒成立，∴ 
，得 
，
综上，实数a的取值范围为 
（3）解：由题意得，fmin（x）+gmax（x）≥2，
∵ 
，∴ 
，即 
，
由 ，
当a≤0时，∵f（1）＜0，则不合题意；
当a＞0时，由f'（x）=0，得 
或x=﹣1（舍去），
当 
时，f'（x）＜0，f（x）单调递减，
当 
时，f'（x）＞0，f（x）单调递增．
∴ 
，即 
，
整理得， 
，
设 
，∴ 
，∴h（x）单调递增，∵a∈Z，∴2a为偶数，
又∵ 
， 
，
∴2a≥4，
故整数a的最小值为2
【解析】（1）根据题意，对f（x）进行求导，由导数的几何意义分析可得y=f（x）在点（1，f（1））处的切线方程，代入点（2,11），计算可得答案，（2）由函数的导数与函数单调性的关系，分函数在（2,3）上单调递增和单调递减两种情况讨论，综合即可得答案，（3）由题意，fmin（x）+gmax（x）≥2，即 f ( x ) = a x 2 + ( 2 a 1 ) x l n x ≥ 
，对f（x）求导后对a进行分类讨论即可得答案.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减才能正确解答此题．
