Question

【题目】在△ABC中，AB=AC，△ABC的外接圆⊙O的弦AD的延长线交BC的延长线于点E．
求证：△ABD∽△AEB．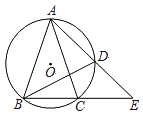

Answer 1

【答案】证明：∵AB=AC，∴∠ABC=∠ACB，

∵∠ACB与∠ADB所对应的弧为 ．

∴∠ACB=∠ADB，

∴∠ADB=∠ABC，

又∠BAD共用，

∴△ABD∽△AEB

【解析】根据同弧所对的圆周角相等可知ACB=ADB，从而得到ADB=ABC，然后根据“如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似”即可证明.
【考点精析】关于本题考查的相似三角形的判定，需要了解相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）才能得出正确答案．