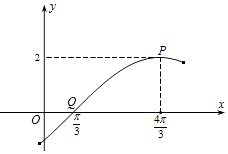题目内容
【题目】已知函数f(x)=a(x+lnx)(a>0),g(x)=x2 .
(1)若f(x)的图象在x=1处的切线恰好也是g(x)图象的切线.求实数a的值;
(2)对于区间[1,2]上的任意两个不相等的实数x1 , x2且x1<x2 , 都有f(x2)﹣f(x1)<g(x2)﹣g(x1)成立.试求实数a的取值范围.
【答案】
(1)解:函数f(x)=a(x+lnx)(a>0), ![]() ,
,
∴x=1,f'(1)=2a,切点为(1,a),
∴切线方程为y﹣a=2a(x﹣1),即y=2ax﹣a,
又联立 ![]() ,消去y,可得x2﹣2ax+a=0,△=4a2﹣4a=0,
,消去y,可得x2﹣2ax+a=0,△=4a2﹣4a=0,
∴a=1
(2)解:由条件可知:f(x2)﹣g(x2)<f(x1)﹣g(x1)(x1<x2),
设F(x)=f(x)﹣g(x),即F(x)=a(x+lnx)﹣x2,
∴F(x)在[1,2]上单调递减,∴ ![]() 在[1,2]上恒成立,
在[1,2]上恒成立,
即 ![]() 在[1,2]上恒成立,∵
在[1,2]上恒成立,∵ ![]() ,
,
∴a≤1,又由条件知a>0,0<a≤1从而即为所求
【解析】(1)对f(x)进行求导,找到在点(1,a)的切线方程,与g(x)联立,根据只有一个交点,解出a的值,(2)设F(x)=f(x)﹣g(x),即F(x)=a(x+lnx)﹣x2,F(x)在[1,2]上单调递减,F ' ( x )0 在[1,2]上恒成立,参变分离后,求出a的取值范围即可.
【考点精析】关于本题考查的利用导数研究函数的单调性,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】已知函数f(x)=(a2﹣3a+3)ax是指数函数,
(1)求f(x)的表达式;
(2)判断F(x)=f(x)﹣f(﹣x)的奇偶性,并加以证明
(3)解不等式:loga(1﹣x)>loga(x+2)
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 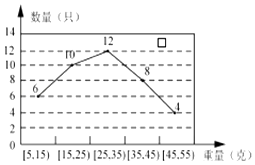
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.