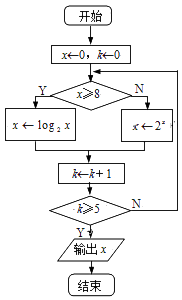
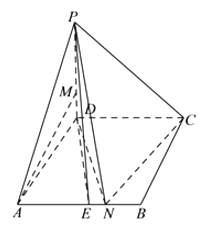
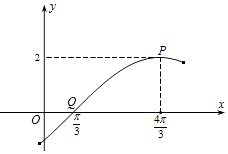题目内容
【题目】在锐角三角形ABC中，9tanAtanB+tanBtanC+tanCtanA的最小值为 ．
【答案】25
【解析】解：如图，不妨设CD=1，AD=m，BD=n，
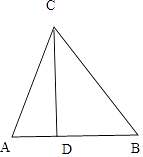
∴tanA= 
，tanB= 
，（m＞0，n＞0），
∴tanC=
tan（A+B）= 
= 
，
∵tanC＞0，
∴mn＜1，
∴9tanAtanB+tanBtanC+tanCtanA= 
+（ + ） ，
= + 
，
≥ + 
，
=（ + ）[mn+（1﹣mn）]，
=9+4+ 
+ 
，
≥13+2 
=13+12=25，当且仅当 = ，即m=n= 
时取等号，
故最小值为25，
所以答案是：25 .
【考点精析】本题主要考查了基本不等式在最值问题中的应用的相关知识点，需要掌握用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”才能正确解答此题．
练习册系列答案
相关题目
