题目内容
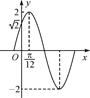
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<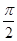 )的周期为π,且图象上有一个最低点为M
)的周期为π,且图象上有一个最低点为M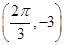 .
.
(1)求f(x)的解析式;
(2)求函数y=f(x)+f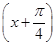 的最大值及对应x的值.
的最大值及对应x的值.
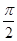 )的周期为π,且图象上有一个最低点为M
)的周期为π,且图象上有一个最低点为M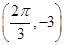 .
.(1)求f(x)的解析式;
(2)求函数y=f(x)+f
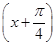 的最大值及对应x的值.
的最大值及对应x的值.(1)f(x)=3sin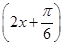 (2)ymax=3
(2)ymax=3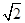 ,x=kπ+
,x=kπ+ ,k∈Z.
,k∈Z.
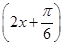 (2)ymax=3
(2)ymax=3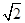 ,x=kπ+
,x=kπ+ ,k∈Z.
,k∈Z.(1)由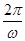 =π,得ω=2.由最低点为M
=π,得ω=2.由最低点为M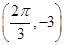 ,得A=3.
,得A=3.
且2×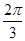 +φ=
+φ=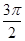 +2kπ(k∈Z),0<φ<
+2kπ(k∈Z),0<φ<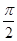 ,
,
∴φ=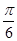 .∴f(x)=3sin
.∴f(x)=3sin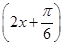 .
.
(2)y=f(x)+f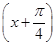 =3sin
=3sin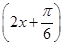 +3sin
+3sin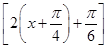
=3sin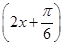 +3cos
+3cos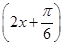 =3
=3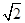 sin
sin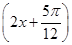 ,
,
∴ymax=3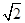 .此时,2x+
.此时,2x+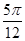 =2kπ+
=2kπ+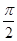 ,即x=kπ+
,即x=kπ+ ,k∈Z.
,k∈Z.
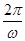 =π,得ω=2.由最低点为M
=π,得ω=2.由最低点为M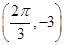 ,得A=3.
,得A=3.且2×
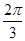 +φ=
+φ=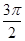 +2kπ(k∈Z),0<φ<
+2kπ(k∈Z),0<φ<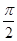 ,
,∴φ=
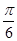 .∴f(x)=3sin
.∴f(x)=3sin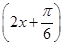 .
.(2)y=f(x)+f
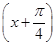 =3sin
=3sin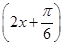 +3sin
+3sin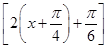
=3sin
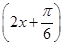 +3cos
+3cos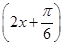 =3
=3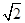 sin
sin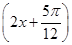 ,
,∴ymax=3
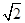 .此时,2x+
.此时,2x+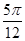 =2kπ+
=2kπ+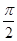 ,即x=kπ+
,即x=kπ+ ,k∈Z.
,k∈Z.
练习册系列答案
相关题目
 、
、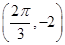 ,则这个函数的解析式为________.
,则这个函数的解析式为________.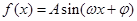 (其中
(其中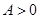 ,
,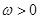 ,
,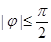 )与坐标轴的三个交点
)与坐标轴的三个交点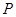 、
、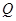 、
、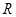 满足
满足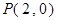 ,
,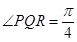 ,
,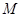 为
为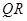 的中点,
的中点,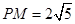 ,则
,则 的值为( )
的值为( )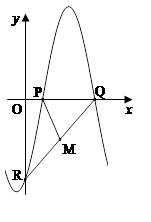
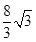

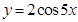 的图像,只需将函数
的图像,只需将函数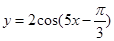 的图像( )
的图像( )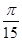 个单位
个单位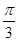 个单位
个单位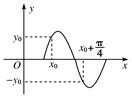
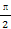 )在y轴右侧依次的前三个交点的横坐标成等比数列,则b的值是 .
)在y轴右侧依次的前三个交点的横坐标成等比数列,则b的值是 .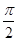 )的部分图象如图所示,则ω=________.
)的部分图象如图所示,则ω=________.