题目内容
19.已知函数f(x)=|2x+1|-|x-3|.(1)解不等式f(x)≤4;
(2)若存在x使得f(x)+a≤0成立,求实数a的取值范围.
分析 (1)作出函数y=|2x+1|-|x-3|的图象,可得它的图象与直线y=4的交点为(-8,4)和(2,4),从而求得|2x+1|-|x-3|≤4的解集.
(2)由y=|2x+1|-|x-3|的图象可知f(x)min=-$\frac{7}{2}$,由题意可得-a≥f(x)min,由此求得实数a的取值范围.
解答 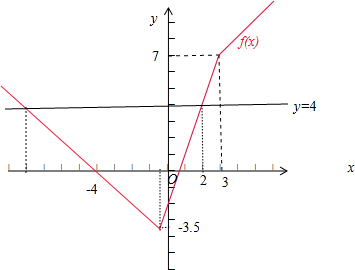 解:(1)y=|2x+1|-|x-3|=$\left\{\begin{array}{l}{-x-4,x≤-\frac{1}{2}}\\{3x-2,-\frac{1}{2}<x<3}\\{x+4,x≥3}\end{array}\right.$,作出函数y=|2x+1|-|x-3|的图象,
解:(1)y=|2x+1|-|x-3|=$\left\{\begin{array}{l}{-x-4,x≤-\frac{1}{2}}\\{3x-2,-\frac{1}{2}<x<3}\\{x+4,x≥3}\end{array}\right.$,作出函数y=|2x+1|-|x-3|的图象,
可得它的图象与直线y=4的交点为(-8,4)和(2,4).
则|2x+1|-|x-3|≤4的解集为[-8,2].
(2)由y=|2x+1|-|x-3|的图象可知当x=-$\frac{1}{2}$时,f(x)min=-$\frac{7}{2}$,
∴存在x使得f(x)+a≤0成立,等价于-a≥f(x)min,
等价于a≤$\frac{7}{2}$.
点评 本题主要考查对由绝对值的函数,绝对值不等式的解法,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.cos17°sin43°+sin17°cos43°( )
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
7.已知△ABC中,a=2,b=4,c=60°,则三角形的形状为( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
4.曲线y=cosx(0≤x≤$\frac{3π}{2}$)与x轴以及直线x=$\frac{3π}{2}$所围图形的面积为( )
| A. | 4 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
 如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点.