题目内容
4.曲线y=cosx(0≤x≤$\frac{3π}{2}$)与x轴以及直线x=$\frac{3π}{2}$所围图形的面积为( )| A. | 4 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
分析 根据所围成图形用定积分可求得曲线y=cosx以及直线x=$\frac{3π}{2}$所围图形部分的面积,然后根据定积分的定义求出所求即可.
解答 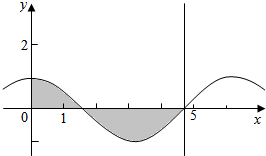 解:由定积分定义及余弦函数的对称性,
解:由定积分定义及余弦函数的对称性,
可得曲线y=cosx以及直线x=$\frac{3π}{2}$所围图形部分的面积为:
S=3∫${\;}_{0}^{\frac{π}{2}}$cosxdx=3sinx|${\;}_{0}^{\frac{π}{2}}$=3sin$\frac{π}{2}$-3sin0=3,
所以围成的封闭图形的面积是3.
故选:D.
点评 本题主要考查了定积分在求面积中的应用,考查运算求解能力,化归与转化思想思想,属于基本知识的应用.

练习册系列答案
相关题目
14.对于函数f(x)=aex+x,若存在实数m,n,使得f(x)≥0的解集为[m,n](m<n),则实数a的取值范围是( )
| A. | (-$\frac{1}{e}$,0)∪(0,+∞) | B. | [-$\frac{1}{e}$)∪(0,+∞) | C. | (-$\frac{1}{e}$,0) | D. | [-$\frac{1}{e}$,0) |
13.设复数z1=1+2i,z2=3-4i,则$\frac{z_1}{z_2}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.已知函数f(x)=sin(ωx+$\frac{π}{4}$)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将函数y=f(x)的图象( )
| A. | 向右平移$\frac{π}{8}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{8}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |