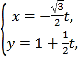题目内容
【题目】2019年12月12日我国出现了新型冠状病毒所感染的肺炎，新型冠状病毒的传染性极强.下图是2020年1月26号到2月17号全国/湖北/非湖北新增新型冠状病毒感染确诊病例对比图，根据图象下列判断错误的是（ ）
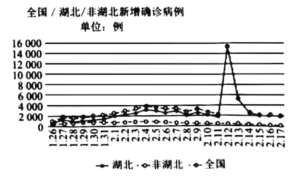
A.该时段非湖北新增感染确诊病例比湖北少
B.全国新增感染确诊病例平均数先增后减
C.2.12全国新增感染确诊病例明显增加，主要是由湖北引起的
D.2.12全国新增感染确诊病例数突然猛增，不会影响该段时期全国新增病例数的中位数
【答案】B
【解析】
根据图象进行分析即可得解.
由图可知A、C正确，2.12之前平均数先增后减，但2.12新增病例数突然猛增，使得平均数也突然增大，但不会影响中位数，选项B错误，D正确.
故选：B.
【题目】已知x与y之间的几组数据如表：
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表数据中y的平均值为2.5，若某同学对m赋了三个值分别为1.5，2，2.5，得到三条线性回归直线方程分别为
，
，
，对应的相关系数分别为
，
，
，下列结论中错误的是（ ）
参考公式：线性回归方程
中，其中
，
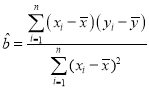．相关系数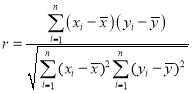
．
A.三条回归直线有共同交点B.相关系数中，最大
C.
D.
【题目】某汽车制造厂制造了某款汽车.为了了解汽车的使用情况，通过问卷的形式，随机对50名客户对该款汽车的喜爱情况进行调查，如图1是汽车使用年限的调查频率分布直方图，如表2是该50名客户对汽车的喜爱情况.
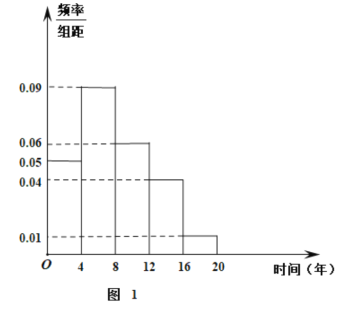
表2
不喜欢该款汽车 | 喜欢该款汽车 | 总计 | |
女士 | 11 | ||
男士 | 23 | 30 | |
总计 |
（1）将表2补充完整，并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢该款汽车与性别有关；
（2）根据图中的数据，甲说：“中位数在
组内”；乙说：“平均数大于中位数”；丙说：“中位数和平均数一样”，针对三位同学的说法，你认为哪种说法合理，给出说明.
附：
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花做垃圾处理．
（Ⅰ）若花店一天购进17枝玫瑰花，求当天的利润y(单位：元)关于当天需求量n（单位：枝，n∈N）的函数解析式．
（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(i)假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润（单位：元）的平均数；
(ii)若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率.
（命题意图）本题主要考查给出样本频数分别表求样本的均值、将频率做概率求互斥事件的和概率，是简单题.