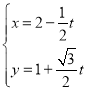题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为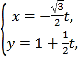 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)求出曲线C1的直角坐标方程为![]() ,设点N(x′,y′),Q(x,y),由中点坐标公式得
,设点N(x′,y′),Q(x,y),由中点坐标公式得![]() ,由此能求出点Q的轨迹C2的直角坐标方程.(2)
,由此能求出点Q的轨迹C2的直角坐标方程.(2)![]() 的坐标为
的坐标为![]() ,设
,设![]() 的参数方程为
的参数方程为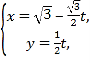 ,(
,( ![]() 为参数)代入曲线
为参数)代入曲线![]() 的直角坐标方程得
的直角坐标方程得![]() ,根据韦达定理,利用t的参数意义得
,根据韦达定理,利用t的参数意义得![]()
即可得解.
试题解析:
(1)由题意知,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
设点![]() ,
, ![]() ,由中点坐标公式得
,由中点坐标公式得![]() ,
,
代入![]() 中,得点
中,得点![]() 的轨迹
的轨迹![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)![]() 的坐标为
的坐标为![]() ,设
,设![]() 的参数方程为
的参数方程为 ,(
,( ![]() 为参数)代入曲线
为参数)代入曲线![]() 的直角坐标方程得:
的直角坐标方程得: ![]() ,
,
设点![]() 对应的参数分别为
对应的参数分别为![]() ,
,
则![]() ,
, ![]() ,
, ![]() .
.

练习册系列答案
相关题目
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了止损,某地一水果店老板利用抖音直播卖货,经过一段时间对一种水果的销售情况进行统计,得到![]() 天的数据如下:
天的数据如下:
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
(1)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)该水果店开展促销活动,当该水果销售单价为![]() 元/
元/![]() 时,其销售量达到
时,其销售量达到![]() ,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过
,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() ,则认为所得到的回归直线方程是理想的,试问:(1)中得到的回归直线方程是否理想?
,则认为所得到的回归直线方程是理想的,试问:(1)中得到的回归直线方程是否理想?
(3)根据(1)的结果,若该水果成本是![]() 元/
元/![]() ,销售单价
,销售单价![]() 为何值时(销售单价不超过
为何值时(销售单价不超过![]() 元/
元/![]() ),该水果店利润的预计值最大?
),该水果店利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中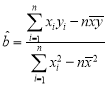 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.