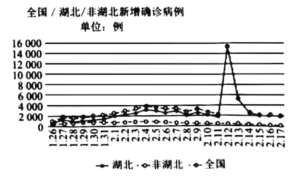
题目内容
【题目】某大型公司为了切实保障员工的健康安全，贯彻好卫生防疫工作的相关要求，决定在全公司范围内举行一次
普查，为此需要抽验1000人的血样进行化验，由于人数较多，检疫部门制定了下列两种可供选择的方案．
方案①：将每个人的血分别化验，这时需要验1000次．
方案②：按
个人一组进行随机分组，把从每组个人抽来的血混合在一起进行检验，如果每个人的血均为阴性，则验出的结果呈阴性，这个人的血只需检验一次（这时认为每个人的血化验
次）；否则，若呈阳性，则需对这个人的血样再分别进行一次化验，这样，该组个人的血总共需要化验
次．
假设此次普查中每个人的血样化验呈阳性的概率为
，且这些人之间的试验反应相互独立．
（1）设方案②中，某组个人的每个人的血化验次数为
，求的分布列；
（2）设
，试比较方案②中，分别取2，3，4时，各需化验的平均总次数；并指出在这三种分组情况下，相比方案①，化验次数最多可以平均减少多少次？（最后结果四舍五入保留整数）
【答案】（1）详解见解析；（2）690，604，594；406.
【解析】
（1）设每个人的血呈阴性反应的概率为
，依题意知
的可能取值，计算分布列即可；
（2）方案②中计算每个人的平均化验次数
，分别求出
、3、4时的值，再与方案①比较，即可得出所求．
解：（1）由题可知，每个人的血样化验呈阳性的概率为
，
设每个人的血呈阴性反应的概率为，则
，
所以
个人的混合后呈阴性的概率为
，呈阳性反应的概率为
，
依题意知的可能取值为
，
，
所以的分布列为；
|
|
|
|
|
|
（2）方案②中，结合（1）知每个人的平均化验次数为：
；
所以当时，
，
此时1000人需要化验的总次数为690次；
当
时，
，
此时1000人需要化验的总次数为604次；
当
时，
，
此时1000人需要化验的总次数为594次；
即时化验次数最多，时化验次数居中，时化验次数最少，
而采用方案①需要化验1000次，
所以在这三种分组情况下，相比方案①，
时化验次数最多可以平均减少
（次
．
