题目内容
已知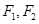 是椭圆的两个焦点,过
是椭圆的两个焦点,过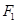 且与椭圆长轴垂直的直线交椭圆于A、B两点,若
且与椭圆长轴垂直的直线交椭圆于A、B两点,若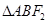 是等腰直角三角形,则这个椭圆的离心率是( )
是等腰直角三角形,则这个椭圆的离心率是( )
A、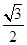 B、
B、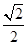 C、
C、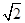 D、
D、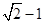
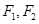 是椭圆的两个焦点,过
是椭圆的两个焦点,过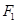 且与椭圆长轴垂直的直线交椭圆于A、B两点,若
且与椭圆长轴垂直的直线交椭圆于A、B两点,若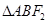 是等腰直角三角形,则这个椭圆的离心率是( )
是等腰直角三角形,则这个椭圆的离心率是( )A、
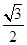 B、
B、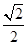 C、
C、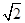 D、
D、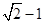
D
由△ABF2是等腰直角三角形可知|AF1|=|F1F2|,即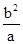 =2c,由此推导出这个椭圆的离心率.
=2c,由此推导出这个椭圆的离心率.
解:由△ABF2是等腰直角三角形可知|AF1|=|F1F2|,∴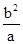 =2c
=2c
又∵c2=a2-b2
∴a2-c2-2ac=0
∴e2+2e-1=0
解之得:e=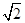 -1或e=-
-1或e=-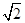 -1 (负值舍去).
-1 (负值舍去).
故选D
题主要考查了椭圆的简单性质.椭圆的离心率是高考中选择填空题常考的题目.应熟练掌握圆锥曲线中a,b,c和e的关系.
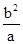 =2c,由此推导出这个椭圆的离心率.
=2c,由此推导出这个椭圆的离心率.解:由△ABF2是等腰直角三角形可知|AF1|=|F1F2|,∴
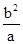 =2c
=2c又∵c2=a2-b2
∴a2-c2-2ac=0
∴e2+2e-1=0
解之得:e=
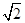 -1或e=-
-1或e=-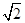 -1 (负值舍去).
-1 (负值舍去).故选D
题主要考查了椭圆的简单性质.椭圆的离心率是高考中选择填空题常考的题目.应熟练掌握圆锥曲线中a,b,c和e的关系.

练习册系列答案
相关题目
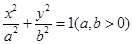 的焦点坐标为
的焦点坐标为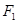 (
(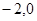 ),点M(
),点M(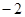 ,
,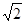 )在椭圆E上.
)在椭圆E上.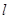 与椭圆E交于
与椭圆E交于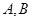 两点,求线段
两点,求线段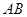 中点
中点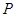 的轨迹方程;
的轨迹方程;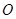 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点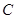 ,
,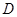 且
且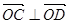 ,求⊙
,求⊙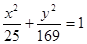 的焦点坐标是( )
的焦点坐标是( )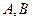 是椭圆
是椭圆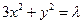 上的两点,点
上的两点,点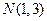 是线段
是线段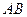 的中点,线段
的中点,线段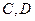 两点.
两点.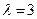 时,过点P(0,1)且倾斜角为
时,过点P(0,1)且倾斜角为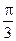 的直线与椭圆相交于E、F两点,求
的直线与椭圆相交于E、F两点,求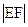 长;
长;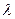 的取值范围,并求直线CD的方程.
的取值范围,并求直线CD的方程.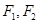 是椭圆
是椭圆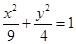 的两个焦点,
的两个焦点,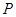 是椭圆上的点,且
是椭圆上的点,且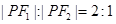 ,则
,则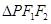 的面积为
的面积为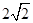
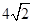
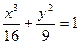 短轴的两个顶点为焦点,且过点
短轴的两个顶点为焦点,且过点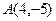 的双曲线的标准方程。
的双曲线的标准方程。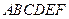 的两个顶点
的两个顶点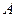 、
、 为椭圆的两个
为椭圆的两个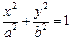 的焦点F,且与椭圆交于相异的两点A、B,则
的焦点F,且与椭圆交于相异的两点A、B,则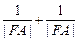 等于常数
等于常数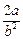 ” 可以类比推出抛物线的类似性质是“若直线l过抛物线
” 可以类比推出抛物线的类似性质是“若直线l过抛物线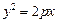 的焦点F,且与抛物线交于相异的两点A、B,则
的焦点F,且与抛物线交于相异的两点A、B,则 的离心率等于__________,与该椭圆有共
的离心率等于__________,与该椭圆有共
 的双曲线方程是
的双曲线方程是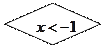
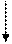

 ___________________.
___________________.