题目内容
(本小题共12分)
已知椭圆E: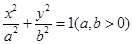 的焦点坐标为
的焦点坐标为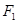 (
(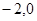 ),点M(
),点M(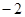 ,
,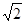 )在椭圆E上.
)在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设Q(1,0),过Q点引直线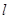 与椭圆E交于
与椭圆E交于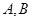 两点,求线段
两点,求线段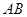 中点
中点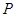 的轨迹方程;
的轨迹方程;
(Ⅲ)O为坐标原点,⊙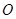 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点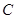 ,
,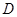 且
且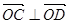 ,求⊙
,求⊙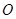 的半径.
的半径.
已知椭圆E:
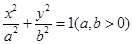 的焦点坐标为
的焦点坐标为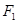 (
(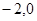 ),点M(
),点M(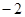 ,
,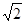 )在椭圆E上.
)在椭圆E上.(Ⅰ)求椭圆E的方程;
(Ⅱ)设Q(1,0),过Q点引直线
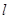 与椭圆E交于
与椭圆E交于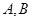 两点,求线段
两点,求线段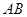 中点
中点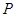 的轨迹方程;
的轨迹方程;(Ⅲ)O为坐标原点,⊙
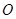 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点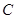 ,
,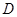 且
且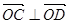 ,求⊙
,求⊙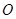 的半径.
的半径.解: (Ⅰ)∵椭圆E:  (a,b>0)经过M(-2,
(a,b>0)经过M(-2, ),一个焦点坐标为
),一个焦点坐标为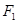 (
(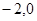 ),∴
),∴ ,椭圆E的方程为
,椭圆E的方程为 ; ……………4分
; ……………4分

 ∵
∵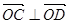 ,∴
,∴ ,即
,即 ,
,
∴ ,即
,即 ,∵直线
,∵直线 为⊙
为⊙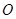 的一条切线,
的一条切线,
∴圆的半径 , 即
, 即 ,
,
经检验,当⊙ 的切线斜率不存在时也成立.∴
的切线斜率不存在时也成立.∴ .…………12分
.…………12分
 (a,b>0)经过M(-2,
(a,b>0)经过M(-2, ),一个焦点坐标为
),一个焦点坐标为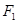 (
(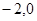 ),∴
),∴ ,椭圆E的方程为
,椭圆E的方程为 ; ……………4分
; ……………4分
 ∵
∵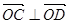 ,∴
,∴ ,即
,即 ,
,∴
 ,即
,即 ,∵直线
,∵直线 为⊙
为⊙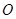 的一条切线,
的一条切线,∴圆的半径
 , 即
, 即 ,
,经检验,当⊙
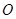 的切线斜率不存在时也成立.∴
的切线斜率不存在时也成立.∴ .…………12分
.…………12分略

练习册系列答案
相关题目
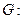
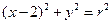 是椭圆
是椭圆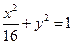 的内接△
的内接△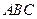 的内切圆, 其中
的内切圆, 其中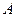 为椭圆的左顶点.
为椭圆的左顶点.
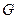 的半径
的半径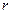 ;
; 2)过点
2)过点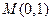 作圆
作圆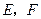 两点,
两点,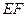 与圆
与圆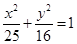 的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( )
的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( )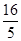

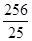
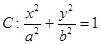 的左焦点作直线
的左焦点作直线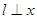 轴,交椭圆C于A,B两点,若△OAB(O为坐标原点)是直角三角形,则椭圆C的离心率e为( )
轴,交椭圆C于A,B两点,若△OAB(O为坐标原点)是直角三角形,则椭圆C的离心率e为( )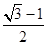
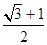
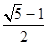
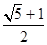
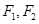 是椭圆的两个焦点,过
是椭圆的两个焦点,过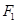 且与椭圆长轴垂直的直线交椭圆于A、B两点,若
且与椭圆长轴垂直的直线交椭圆于A、B两点,若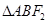 是等腰直角三角形,则这个椭圆的离心率是( )
是等腰直角三角形,则这个椭圆的离心率是( )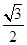 B、
B、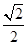 C、
C、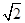 D、
D、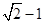
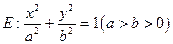 过点
过点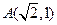 ,且点
,且点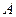 在
在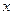 轴上的射影恰为椭圆的一个焦点
轴上的射影恰为椭圆的一个焦点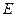 的方程;
的方程;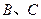 两点.试问:四边形
两点.试问:四边形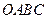 能否为平行四边形?若能,求出直线
能否为平行四边形?若能,求出直线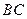 的方程;否则说明理由.
的方程;否则说明理由.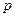 :方程
:方程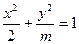 表示焦点在
表示焦点在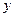 轴上的椭圆,命题
轴上的椭圆,命题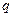 :关于x的方程
:关于x的方程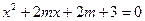 无实根,若“
无实根,若“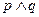 ”为假命题,“
”为假命题,“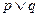 ”为真命题,求实数
”为真命题,求实数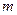 的取值范围.
的取值范围.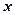 轴上的椭圆
轴上的椭圆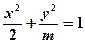 的离心率为
的离心率为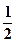 ,则m=" "
,则m=" " 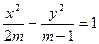 表示焦点在
表示焦点在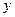 轴上的椭圆,则
轴上的椭圆,则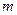 的取值范围是_____
的取值范围是_____