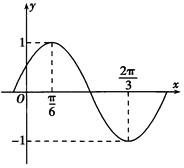
题目内容
【题目】在△ABC中,若acosA﹣bcosB=0,则三角形的形状是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
【答案】D
【解析】解:法1:∵cosA= ![]() ,cosB=
,cosB= ![]() , ∴
, ∴ ![]() a=
a= ![]() b,
b,
化简得:a2c2﹣a4=b2c2﹣b4 , 即(a2﹣b2)c2=(a2﹣b2)(a2+b2),
①若a2﹣b2=0时,a=b,此时△ABC是等腰三角形;
②若a2﹣b2≠0,a2+b2=c2 , 此时△ABC是直角三角形,
所以△ABC是等腰三角形或直角三角形;
法2:根据正弦定理可知∵acosA=bcosB,
∴sinAcosA=sinBcosB,
∴sin2A=sin2B,
∴A=B,或2A+2B=180°即A+B=90°,
所以△ABC为等腰或直角三角形.
故选D
解法1:把由余弦定理解出的余弦表达式代入已知的等式化简可得:(a2﹣b2)c2=(a2﹣b2)(a2+b2),分①a2﹣b2=0和②a2﹣b2≠0两种情况讨论;
解法2:根据正弦定理把等式acosA=bcosB的边换成角的正弦,再利用倍角公式化简整理得sin2A=sin2B,进而推断A=B,或A+B=90°答案可得.

【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该分店此次抽奖活动自开业始,持续![]() 天,参加抽奖的每位顾客抽到一等奖(价值
天,参加抽奖的每位顾客抽到一等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到二等奖(价值
,抽到二等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到三等奖(价值
,抽到三等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() .
.
试估计该分店在此次抽奖活动结束时送出多少元奖品?
参考公式: 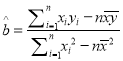 ,
, ![]() .
.