题目内容
已知平行四边形的两条边所在直线的方程分别是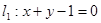 ,
,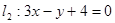 , 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
, 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
其他两边所在直线的方程是3x-y-16=0,x+y-11=0.
解析试题分析:依题意,由方程组x+y?1=0,3x?y+4=0,可解得平行四边形ABCD的顶点A的坐标,再结合对角线的交点是M(3,3),可求得C点坐标,利用点斜式即可求得其他两边所在直线的方程.
试题解析:联立方程组x+y?1=0,3x?y+4=0,
解得x=?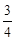 ,y=
,y=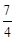 ,
,
所以平行四边形ABCD的顶点A(?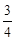 ,
,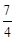 ),
),
设C(x0,y0),由题意,点M(3,3)是线段AC的中点,
∴x0?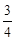 =6,y0+
=6,y0+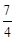 =6,
=6,
解得x0= ,y0=
,y0=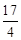 ,
,
∴C( ,
,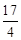 ),
),
由已知,直线AD的斜率kAD=3.
∵直线BC∥AD,
∴直线BC的方程为3x-y-16=0,
由已知,直线AB的斜率kAB=-1,
∵直线CD∥AB,
∴直线CD的方程为x+y-11="0,"
因此,其他两边所在直线的方程是3x-y-16=0,x+y-11=0.
考点:1.直线的一般式方程与直线的平行关系;2.直线的一般式方程.

练习册系列答案
相关题目
 :
: 内有一点
内有一点 ,过点
,过点 作直线
作直线 交圆
交圆 ,
, 两点.
两点. 被点
被点 :
: ,(
,( 不同时为0),
不同时为0), :
: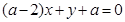 ,
, 且
且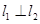 ,求实数
,求实数 的值;
的值; 且
且 时,求直线
时,求直线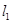 :
: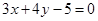 与直线
与直线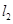 :
: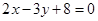 的交点
的交点 ,且满足下列条件的直线方程
,且满足下列条件的直线方程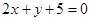 平行 ;
平行 ;  平行且距离等于
平行且距离等于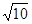 的直线方程。
的直线方程。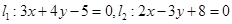 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程: 交于
交于 两点.
两点. 上的圆的方程.
上的圆的方程.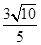 的直线方程.
的直线方程. 、
、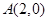 、
、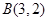 ,
,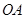 边上的中线所在直线为
边上的中线所在直线为 .(1)求
.(1)求