题目内容
求曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离.
曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是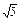
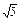
设曲线上过点P（x0,y0）的切线平行于直线2x-y+3=0，即斜率是2，则y′|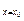
=
=
|=
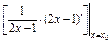
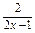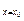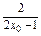=2.
解得x0=1,所以y0=0,即点P（1，0），
点P到直线2x-y+3=0的距离为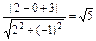
,
∴曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是.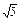
==
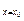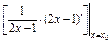
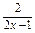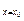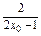|==2.解得x0=1,所以y0=0,即点P（1，0），
点P到直线2x-y+3=0的距离为
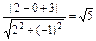,∴曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是
.
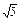练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
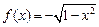在区间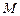
上的反函数是其本身，则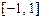
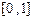
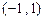
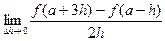； （2）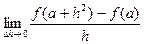
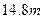的钢条做一个长方体容器的框架.如果所做容器的低面的一边长比另以一边长多
那么高是多少时容器的容积最大,并求出它的最大容积.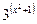 
的值域为_________.
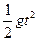，（1）计算t从3秒到3.1秒内平均速度；（2）求t=3秒是瞬时速度。
x3＋x
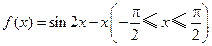的最值。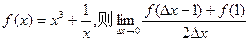
= .