题目内容
17.如果数列a1,$\frac{a_2}{a_1}$,$\frac{a_3}{a_2}$,…,$\frac{a_n}{{{a_{n-1}}}}$,…是首项为1,公比为$\sqrt{2}$的等比数列,${b_n}=\frac{1}{{{{log}_2}{a_n}}}$,n≥2,$\lim_{n→∞}({b_2}+{b_3}…+{b_n})$=4.分析 运用等比数列的通项和恒等式an=a1•$\frac{a_2}{a_1}$•$\frac{a_3}{a_2}$•…•$\frac{a_n}{{{a_{n-1}}}}$,化简整理,再由对数的运算性质和裂项相消求和,结合数列极限的性质,即可计算得到.
解答 解:由题意可得an=a1•$\frac{a_2}{a_1}$•$\frac{a_3}{a_2}$•…•$\frac{a_n}{{{a_{n-1}}}}$=1•$\sqrt{2}$•($\sqrt{2}$)2•…•($\sqrt{2}$)n-1
=$(\sqrt{2})^{\frac{n(n-1)}{2}}$,
${b_n}=\frac{1}{{{{log}_2}{a_n}}}$=$\frac{1}{\frac{n(n-1)}{2}lo{g}_{2}\sqrt{2}}$=$\frac{4}{n(n-1)}$=4($\frac{1}{n-1}$-$\frac{1}{n}$),
即有$\lim_{n→∞}({b_2}+{b_3}…+{b_n})$=$\underset{lim}{n→∞}$4(1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$)
=$\underset{lim}{n→∞}$4(1-$\frac{1}{n}$)=4-4$\underset{lim}{n→∞}\frac{1}{n}$=4-0=4.
故答案为:4.
点评 本题考查等比数列的通项和数列恒等式的运用,同时考查数列求和的方法:裂项相消求和,考查数列极限的运算求解能力,属于中档题.

练习册系列答案
相关题目
7.已知二次函数f(x)的二次项系数为正数,且对任意x∈R,都有f(x)=f(4-x)成立,若f(1-2x2)<f(1+2x-x2),则实数x的取值范围是( )
| A. | (2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0) | D. | (-∞,-2)∪(0,+∞) |
8.设m,n为空间两条不同的直线,α,β为空间两个不同的平面,给出下列命题:
①若m∥α,m∥β,则α∥β;
②若m∥α,m∥n则n∥α;
③若m⊥α,m∥β,则α⊥β;
④若m⊥α,α∥β,则m⊥β.
其中的正确命题序号是( )
①若m∥α,m∥β,则α∥β;
②若m∥α,m∥n则n∥α;
③若m⊥α,m∥β,则α⊥β;
④若m⊥α,α∥β,则m⊥β.
其中的正确命题序号是( )
| A. | ③④ | B. | ②④ | C. | ①② | D. | ①③ |
6.已知函数f(x)满足条件:?x∈R,f(x)+f(-x)=0且f(x+t)-f(x)<0(其中t为正数),则函数f(x)的解析式可以是( )
| A. | y=$\frac{1}{x}$ | B. | y=x3 | C. | y=sinx | D. | y=-3x |
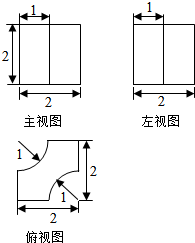
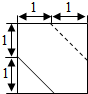
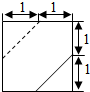
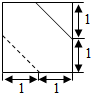
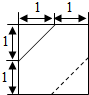
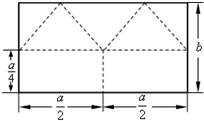 边长分别为a、b的矩形,按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接成该正四棱锥的4个侧面,则$\frac{b}{a}$的取值范围是($\frac{1}{2}$,+∞).
边长分别为a、b的矩形,按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接成该正四棱锥的4个侧面,则$\frac{b}{a}$的取值范围是($\frac{1}{2}$,+∞).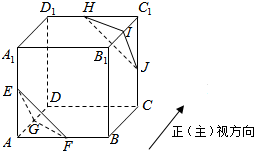 已知正方体ABCD-A1B1C1D1的棱长为2,点E,F,G,H,I,J分别是该正方体的棱AA1,AB,AD,C1D1,C1B1,C1C的中点,现从该正方体中截去棱锥A-EFG与棱锥C1-HIJ,若正(主)视方向如图所示,则剩余部分的几何体的侧(左)视图为( )
已知正方体ABCD-A1B1C1D1的棱长为2,点E,F,G,H,I,J分别是该正方体的棱AA1,AB,AD,C1D1,C1B1,C1C的中点,现从该正方体中截去棱锥A-EFG与棱锥C1-HIJ,若正(主)视方向如图所示,则剩余部分的几何体的侧(左)视图为( )