题目内容
19.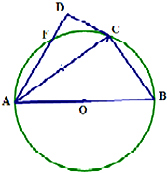 已知AB是⊙O的直径,F为圆上一点,∠BAF的角平分线与圆交于点C,过点C作圆的切线与直线AF相交于点D,若AB=6,∠DAB=$\frac{π}{3}$
已知AB是⊙O的直径,F为圆上一点,∠BAF的角平分线与圆交于点C,过点C作圆的切线与直线AF相交于点D,若AB=6,∠DAB=$\frac{π}{3}$(1)证明:AD⊥CD;
(2)求DF•DA的值及四边形ABCD的面积.
分析 (1)由AB是圆O的直径,可得∠ACB=$\frac{π}{2}$.由于∠DAB=$\frac{π}{3}$,AC平分∠DAB.利用角平分线的性质可得∠CAB=∠CAD=$\frac{π}{6}$,可得∠ABC=$\frac{π}{3}$.利用切线的性质可得∠ACD=∠ABC=$\frac{π}{3}$.可得∠ADC=$\frac{π}{2}$即可.
(2)在Rt△ABC中,利用AB=6,∠ABC=$\frac{π}{3}$,可得AC=ABsin$\frac{π}{3}$=3$\sqrt{3}$.在Rt△ACD中,DC=AC•cos∠ACD.再利用切割线定理可得:DF•DA=DC2即可,再求四边形ABCD的面积.
解答 (1)证明:如图所示.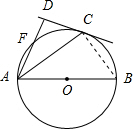
∵AB是圆O的直径,∴∠ACB=$\frac{π}{2}$.
∵∠DAB=$\frac{π}{3}$,AC平分∠DAB.
∴∠CAB=∠CAD=$\frac{π}{6}$,∴∠ABC=$\frac{π}{3}$.
∵DC与⊙O相切于点C,∴∠ACD=∠ABC=$\frac{π}{3}$.
∴∠CAD+∠ACD=$\frac{π}{2}$.
∴∠ADC=$\frac{π}{2}$.
∴AD⊥DC.
(2)解:在Rt△ABC中,∵AB=6,∠ABC=$\frac{π}{3}$.
∴AC=ABsin$\frac{π}{3}$=3$\sqrt{3}$.
在Rt△ACD中,DC=AC•cos∠ACD=3$\sqrt{3}$×$\frac{1}{2}$=$\frac{3\sqrt{3}}{2}$.
由切割线定理可得:DF•DA=DC2=$\frac{27}{4}$.
AF=cos30°•AC=$\frac{9}{2}$,
∴S四边形ABCD=$\frac{1}{2}CD•AD+\frac{1}{2}AC•BC$=$\frac{1}{2}•\frac{3\sqrt{3}}{2}•(\frac{\sqrt{3}}{2}•3\sqrt{3})+\frac{1}{2}•3\sqrt{3}•3$=$\frac{63\sqrt{3}}{8}$.
点评 本题中考查了圆的性质、切线的性质、直角三角形的边角关系、角平分线的性质、切割线定理等基础知识与基本技能,属于中档题.

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案| A. | (2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0) | D. | (-∞,-2)∪(0,+∞) |
| A. | 甲得9张,乙得3张 | B. | 甲得6张,乙得6张 | ||
| C. | 甲得8张,乙得4张 | D. | 甲得10张,乙得2张 |
| A. | 1 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 2 |
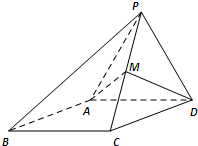 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点,N为AC中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点,N为AC中点.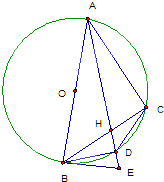 如图,圆O的直径AB、BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
如图,圆O的直径AB、BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.