题目内容
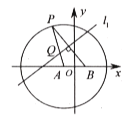
【题目】如图所示,三棱柱![]() 的侧面
的侧面![]() 是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点。
是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点。
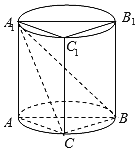
(1)若圆柱的轴截面是正方形,当点C是弧AB的中点时,求异面直线![]() 与AB的所成角的大小(结果用反三角函数值表示);
与AB的所成角的大小(结果用反三角函数值表示);
(2)当点C是弧AB的中点时,求四棱锥![]() 体积与圆柱体积的比.
体积与圆柱体积的比.
【答案】(1) ![]() ;
;
(2) 四棱锥![]() 体积与圆柱体积的比为
体积与圆柱体积的比为![]() .
.
【解析】
(1)根据平行关系找到异面直线所成的角,利用余弦定理即可求解;
(2)先利用线面垂直的判定定理证明![]() 平面
平面![]() ,即得四棱锥
,即得四棱锥![]() 的高,然后利用体积公式即可求解.
的高,然后利用体积公式即可求解.
(1) 连接![]() ,
,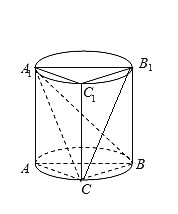 由
由![]() ,可得
,可得![]() 即为异面直线
即为异面直线![]() 与
与![]() 的所成的角或补角,不妨设
的所成的角或补角,不妨设![]() ,则
,则![]() ,在△
,在△![]() 中,由余弦定理知,
中,由余弦定理知,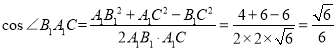 ,故异面直线
,故异面直线![]() 与
与![]() 的所成角的大小为
的所成角的大小为![]() .
.
(2) 由![]() 为直径,可得
为直径,可得![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,故四棱锥
,故四棱锥![]() 体积
体积![]() ,圆柱的体积为
,圆柱的体积为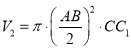 ,又
,又![]() ,所以四棱锥
,所以四棱锥![]() 体积与圆柱体积的比为
体积与圆柱体积的比为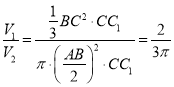 .
.

练习册系列答案
相关题目