题目内容
【题目】已知函数![]() .
.
(I)当![]() 时,求过点(0,1)且和曲线
时,求过点(0,1)且和曲线![]() 相切的直线方程;
相切的直线方程;
(2)若函数![]() 在
在![]() 上有两个不同的零点,求实致
上有两个不同的零点,求实致![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() (2)
(2)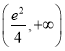
【解析】
(1)讨论点![]() 是否是切点,是切点时,求出在该点的导函数就是切线的斜率,再运用直线的点斜式得切线方程;
是否是切点,是切点时,求出在该点的导函数就是切线的斜率,再运用直线的点斜式得切线方程;
不是切点时,设切点坐标,建立方程求出切点坐标,再求出切线方程;
(2)方法一:将![]() 整理成
整理成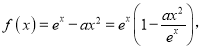 令
令![]() ,对
,对![]() 求导,讨论其零点的个数,就是函数
求导,讨论其零点的个数,就是函数![]() 的零点的个数,注意当
的零点的个数,注意当![]() 最小值小于零时,需对取得最小值的点的左右两侧的函数判断是否有零点的存在,可求出特殊点的函数值判断其正负,根据零点存在定理判断零点的存在;
最小值小于零时,需对取得最小值的点的左右两侧的函数判断是否有零点的存在,可求出特殊点的函数值判断其正负,根据零点存在定理判断零点的存在;
方法二:由![]() 可得
可得![]() 对a实行参变分离方法,构造新函数
对a实行参变分离方法,构造新函数![]() ,对其求导研究此函数的单调性和最值,要使函数
,对其求导研究此函数的单调性和最值,要使函数![]() 在
在![]() 上有两个不同的零点,即直线
上有两个不同的零点,即直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同的交点,可得解.
上有两个不同的交点,可得解.
(1)当![]() 时,
时,![]() ,
,
当点![]() 为切点时,所求直线的斜率为
为切点时,所求直线的斜率为![]() ,则过点
,则过点![]() 且和曲线
且和曲线![]() 相切的直线方程为
相切的直线方程为![]()
当点![]() 不是切点时,设切点坐标为
不是切点时,设切点坐标为![]() ,
,
则所求直线的斜率为![]() ,所以
,所以![]() ,①易知
,①易知![]() ②
②
由①②可得![]()
即![]()
设![]() 则
则![]()
所以当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又![]()
所以![]() 有唯一的零点
有唯一的零点![]() ,
,
因为![]() ,所以方程
,所以方程![]() 的根为
的根为![]() ,即切点坐标为
,即切点坐标为![]() ,
,
故所求切线的斜率为![]() ,则过点
,则过点![]() 且和曲线
且和曲线![]() 相切的直线方程为
相切的直线方程为![]() .
.
综上,所求直线的方程为![]() 或
或![]() .
.
(2)解法一: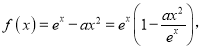 令
令![]() ,
,
因为![]() ,所以函数
,所以函数![]() 的零点就是函数
的零点就是函数![]() 的零点,
的零点,
当![]() 时,
时,![]() 没有零点,所以
没有零点,所以![]() 没有零点.
没有零点.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() 是函数
是函数![]() 在
在![]() 上的最小值.
上的最小值.
当![]() 即
即![]() 在
在![]() 上没有零点,即
上没有零点,即![]() 在
在![]() 上没有零点;
上没有零点;
当![]() 即
即![]() 在
在![]() 上只有一个零点,即即
上只有一个零点,即即![]() 在
在![]() 上只有一个零点;
上只有一个零点;
当![]() 即
即![]() ,即
,即![]() 在
在![]() 上有一个零点,所以
上有一个零点,所以![]() 在
在![]() 上有一个零点;
上有一个零点;
对任意的![]() ,都有
,都有![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]()
故![]() 在
在![]() 上有一个零点,
上有一个零点,
因此![]() 在
在![]() 上有两个不同的零点,即
上有两个不同的零点,即![]() 在
在![]() 上有两个不同的零点.
上有两个不同的零点.
综上,若函数![]() 在
在![]() 上有两个不同的零点,则实数
上有两个不同的零点,则实数![]() 的取值范围是
的取值范围是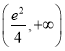 .
.
解法二:由![]() 可得
可得![]()
令![]() ,
,
则函数![]() 在
在![]() 上有两个不同的零点,即直线
上有两个不同的零点,即直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同的交点,
上有两个不同的交点,![]() 令
令![]() 得
得![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 上的最大值为
上的最大值为![]()
因为![]() ,并且当
,并且当![]() 时,
时,![]()
所以当![]() 时,
时,![]() 在
在![]() 上的图象与直线
上的图象与直线![]() 有两个不同的交点,
有两个不同的交点,
即当![]() 时,函数
时,函数![]() 在
在![]() 上有两个不同的零点.
上有两个不同的零点.
所以,若函数![]() 在
在![]() 上有两个不同的零点,则实数a的取值范围是
上有两个不同的零点,则实数a的取值范围是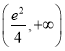 .
.