题目内容
【题目】已知等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,公差
,公差![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,![]() ;数列
;数列![]() 满足:对于任意的
满足:对于任意的![]() ,等式
,等式![]() 都成立.
都成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等比数列;
是等比数列;
(3)若数列![]() 满足
满足![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
【答案】(1)![]() ;(2)证明见解析;(3)存在
;(2)证明见解析;(3)存在
【解析】
(1)将已知条件转化为![]() 的形式列方程组,解方程组求得
的形式列方程组,解方程组求得![]() ,由此求得数列
,由此求得数列![]() 的通项公式.
的通项公式.
(2)根据递推关系式![]() 进行作差变形,求得
进行作差变形,求得![]() ,由此证得数列
,由此证得数列![]() 是等比数列.
是等比数列.
(3)根据![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,![]() ,
,![]() 成等差数列,由(2)求得
成等差数列,由(2)求得![]() ,由此求得
,由此求得![]() ,
,![]() ,根据
,根据![]() 单调递减,对
单调递减,对![]() 进行分类讨论,由此求得
进行分类讨论,由此求得![]() 的值.
的值.
(1)设数列![]() 公差为
公差为![]() ,由题设得
,由题设得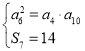 .
.
即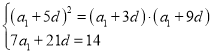 ,解得
,解得![]() .
.
∴数列![]() 的通项公式为:
的通项公式为:![]() .
.
(2)∵![]()
∴![]() ,①
,①
∴![]() ,②
,②
由![]() 得,
得,![]() ③
③
∴![]() ,④
,④
由![]() 得
得![]() ,由①知
,由①知![]() ,
,![]() ,∴
,∴![]() .
.
又![]() ,∴数列
,∴数列![]() 是等比数列.
是等比数列.
(3)假设存在正整数![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
由(2)可知:![]() ,∴
,∴![]() .
.
于是,![]() .
.
由于![]() ,所以
,所以![]()
因为当![]() 时,
时,![]() ,即
,即![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() ,不符合条件,
,不符合条件,
所以![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]()
当![]() 时,得
时,得![]() ,无解,
,无解,
当![]() 时,得
时,得![]() ,所以
,所以![]() ,
,
综上:存在唯一正整数数组![]() ,使
,使![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
【题目】某班随机抽查了![]() 名学生的数学成绩,分数制成如图的茎叶图,其中
名学生的数学成绩,分数制成如图的茎叶图,其中![]() 组学生每天学习数学时间不足
组学生每天学习数学时间不足![]() 个小时,
个小时,![]() 组学生每天学习数学时间达到一个小时,学校规定
组学生每天学习数学时间达到一个小时,学校规定![]() 分及
分及![]() 分以上记为优秀,
分以上记为优秀,![]() 分及
分及![]() 分以上记为达标,
分以上记为达标,![]() 分以下记为未达标.
分以下记为未达标.
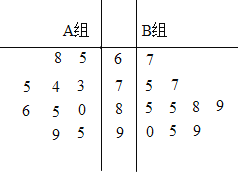
(1)根据茎叶图完成下面的列联表:
达标 | 未达标 | 总计 | |
| |||
| |||
总计 |
(2)判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表: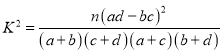 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|