��Ŀ����
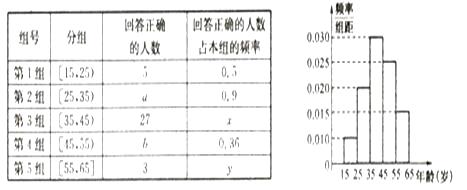
����Ŀ��ij���չ�˾��һ��ղ�Ʒ����ʷ�����ʣ�������=����±������룩��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
�����Թ���ƽ�������ʣ�
�����ݾ��飬��ÿ�ݱ����ı�����20Ԫ�Ļ�����ÿ����![]() Ԫ����Ӧ������
Ԫ����Ӧ������![]() ����ݣ���
����ݣ���![]() ��Ԫ���н�ǿ������ع�ϵ������ʷ���ۼ�¼�г����õ�����5��
��Ԫ���н�ǿ������ع�ϵ������ʷ���ۼ�¼�г����õ�����5��![]() ��
��![]() �Ķ�Ӧ���ݣ�
�Ķ�Ӧ���ݣ�

�ݴ˼�����Ļع鷽��Ϊ![]() .
.
��i�������![]() �Ĺ���ֵ��
�Ĺ���ֵ��
��ii�����ѻع鷽��![]() ����
����![]() ��
��![]() �����Թ�ϵ���ã����������ƽ�������ʹ��ƴ˲�Ʒ�������ʣ�ÿ�ݱ����ı��Ѷ�Ϊ����Ԫʱ�˲�Ʒ�ɻ��������棬��������������.
�����Թ�ϵ���ã����������ƽ�������ʹ��ƴ˲�Ʒ�������ʣ�ÿ�ݱ����ı��Ѷ�Ϊ����Ԫʱ�˲�Ʒ�ɻ��������棬��������������.
���𰸡�����![]() ;����i��
;����i��![]() ,��ii��������.
,��ii��������.
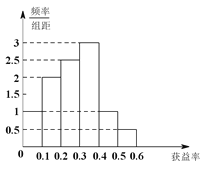
�������������������1���ȸ���Ƶ�ʷֲ�ֱ��ͼ��С������������ڶ�Ӧ������������,�ٸ�������ֵ���Ӧ������ʳ˻��ĺ�Ϊƽ�����ɵ�ƽ��������,��2����i�����ݻع鷽�̹���![]() ,�ȸ���������ƽ��ֵ,�ٴ���ع鷽�������
,�ȸ���������ƽ��ֵ,�ٴ���ع鷽�������![]() �Ĺ���ֵ����ii���ȸ����������������ÿ�ݱ����ı��ѳ˻���һ��һԪ���κ���,���ݶ��κ����Գ���ȷ��������ֵ.
�Ĺ���ֵ����ii���ȸ����������������ÿ�ݱ����ı��ѳ˻���һ��һԪ���κ���,���ݶ��κ����Գ���ȷ��������ֵ.
�������������������ֵ����Ϊ��0.05��0.15��0.25��0.35��0.45��0.55��
ȡֵ��������Ϊ��0.1��0.2��0.25��0.3��0.1��0.05��
ƽ��������Ϊ![]()
![]()
![]()
![]()
![]() .
.
����i��![]()
![]()
![]()
![]()
����![]()
��ii����ÿ�ݱ����ı���Ϊ![]() Ԫ��������Ϊ
Ԫ��������Ϊ![]() ��������Ϊ
��������Ϊ
![]()
![]() ��Ԫ��
��Ԫ��
![]()
![]()
��![]() Ԫʱ�������������Ϊ360��Ԫ��
Ԫʱ�������������Ϊ360��Ԫ��
���չ�˾Ԥ�ƻ���Ϊ![]() ��Ԫ.
��Ԫ.