题目内容
19.已知数列{an}的前n项和为Sn,满足3Sn=an-1.(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=$\frac{{{a}_{n}}^{2}}{1-{a}_{n}}$,数列{bn}前n项的和为Tn,证明:Tn<$\frac{1}{3}$.
分析 (Ⅰ)通过3Sn=an-1,可得首项a1=-$\frac{1}{2}$,3Sn-3Sn-1=an-an-1,即an=$-\frac{1}{2}{a_{n-1}}$,计算即可;
(Ⅱ)通过${a_n}={(-\frac{1}{2})^n}$,利用放缩法、等比数列的求和公式计算即可.
解答 解:(Ⅰ)由3Sn=an-1,得a1=S1=-$\frac{1}{2}$,
当n≥2时,3Sn-1=an-1-1,
两式相减得3Sn-3Sn-1=an-an-1,即an=$-\frac{1}{2}{a_{n-1}}$,
∴数列{an}是首项a1=-$\frac{1}{2}$,公式q=-$\frac{1}{2}$的等比数列,
∴${a_n}={(-\frac{1}{2})^n}$;
(Ⅱ)∵${a_n}={(-\frac{1}{2})^n}$,${b_n}=\frac{{\frac{1}{4^n}}}{{1-{{(-\frac{1}{2})}^n}}}=\frac{1}{{{4^n}-{{(-2)}^n}}}≤\frac{1}{{3•{2^n}}}$,
∴Tn=b1+b2+…bn
$≤\frac{1}{3•2}+\frac{1}{{3•{2^2}}}+…+\frac{1}{{3•{2^n}}}=\frac{1}{3}•\frac{{\frac{1}{2}(1-\frac{1}{2^2})}}{{1-\frac{1}{2}}}=\frac{1}{3}(1-\frac{1}{2^n})<\frac{1}{3}$.
点评 本题考查求数列的通项、判定和的范围,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
9.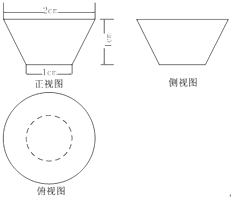 某几何体的三视图如图所示,则该几何体的体积为( )(单位cm3).
某几何体的三视图如图所示,则该几何体的体积为( )(单位cm3).
 某几何体的三视图如图所示,则该几何体的体积为( )(单位cm3).
某几何体的三视图如图所示,则该几何体的体积为( )(单位cm3).| A. | $\frac{7}{12}π$ | B. | $\frac{7π}{3}$ | C. | $2\sqrt{2}π$ | D. | 3π |
10.设函数f(x),g(x)的定义域都为R,且f(x)为奇函数,g(x)为偶函数,则下列结论中正确的是( )
| A. | f(x)sinx为奇函数 | B. | f(x)+cosx为偶函数 | ||
| C. | g(x)sinx为为偶函数 | D. | g(x)+cosx为偶函数 |
9.已知 F1,F2分别是双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右焦点,过 F1,的直线l与双曲线的左右两支分别交于点A,B,若|AB|=|AF2|,∠F1AF2=90°,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{6}+\sqrt{3}}}{2}$ | B. | $\sqrt{6}+\sqrt{3}$ | C. | $\frac{{\sqrt{5+2\sqrt{2}}}}{2}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
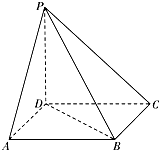 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.