题目内容
9.已知 F1,F2分别是双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右焦点,过 F1,的直线l与双曲线的左右两支分别交于点A,B,若|AB|=|AF2|,∠F1AF2=90°,则双曲线的离心率为( )| A. | $\frac{{\sqrt{6}+\sqrt{3}}}{2}$ | B. | $\sqrt{6}+\sqrt{3}$ | C. | $\frac{{\sqrt{5+2\sqrt{2}}}}{2}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
分析 通过设|AF2|=t,利用勾股定理及双曲线的定义可得t=$\frac{2\sqrt{6}}{3}$c,利用离心率的计算公式计算即可.
解答 解:设|AF2|=t,由题可知:|AB|=t,|BF2|=$\sqrt{2}$t,
则|AF1|=$\sqrt{|{F}_{1}{F}_{2}{|}^{2}-|A{F}_{2}{|}^{2}}$=$\sqrt{4{c}^{2}-{t}^{2}}$,
由双曲线的定义可知:t-$\sqrt{4{c}^{2}-{t}^{2}}$=t+$\sqrt{4{c}^{2}-{t}^{2}}$-$\sqrt{2}$t,
解得:t=$\frac{2\sqrt{6}}{3}$c,
∴|AF1|=$\frac{2\sqrt{3}}{3}$c,
∵|AF2|-|AF1|=2a,即($\frac{2\sqrt{6}}{3}$-$\frac{2\sqrt{3}}{3}$)c=2a,
∴e=$\frac{c}{a}$=$\frac{3}{\sqrt{6}-\sqrt{3}}$=$\sqrt{6}+\sqrt{3}$,
故选:B.
点评 本题考查考查双曲线的离心率,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤8}\\{2y-x≤4}\\{x≥0}\\{y≥0}\end{array}\right.$,且z=4y-x的最大值为a,最小值为b,则a+b的值是( )
| A. | 10 | B. | 20 | C. | 4 | D. | 12 |
4.设{an}是等比数列,则对任何n∈N*,都有$\frac{1}{{{a_1}{a_2}}}•\frac{1}{{{a_2}{a_3}}}…\frac{1}{{{a_n}{a_{n+1}}}}$=( )
| A. | $\frac{1}{{{{({a_1}•{a_n})}^n}}}$ | B. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^n}}}$ | C. | $\frac{1}{{{{({a_1}•{a_n})}^{n+1}}}}$ | D. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^{n+1}}}}$ |
19.将甲,乙等5位同学分别保送到北京大学,复旦大学,中国科技大学就读,则每所大学至少保送一人的不同保送的方法数共有( )种.
| A. | 240 | B. | 180 | C. | 150 | D. | 540 |
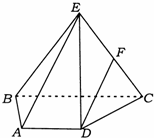 已知四棱锥E-A BCD中,AD∥BC,AD=$\frac{1}{2}$BC=1,△BCE为等边三角形,且面BCE⊥面ABCD,点F为CE中点.
已知四棱锥E-A BCD中,AD∥BC,AD=$\frac{1}{2}$BC=1,△BCE为等边三角形,且面BCE⊥面ABCD,点F为CE中点.