题目内容
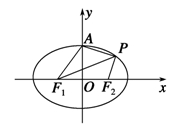
如图,椭圆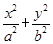 =1(a>b>0)的左、右焦点为F1,F2,上顶点为A,离心率为
=1(a>b>0)的左、右焦点为F1,F2,上顶点为A,离心率为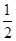 ,点P为第一象限内椭圆上的一点,若S△PF1A∶S△PF1F2=2∶1,则直线PF1的斜率为________.
,点P为第一象限内椭圆上的一点,若S△PF1A∶S△PF1F2=2∶1,则直线PF1的斜率为________.
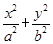 =1(a>b>0)的左、右焦点为F1,F2,上顶点为A,离心率为
=1(a>b>0)的左、右焦点为F1,F2,上顶点为A,离心率为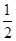 ,点P为第一象限内椭圆上的一点,若S△PF1A∶S△PF1F2=2∶1,则直线PF1的斜率为________.
,点P为第一象限内椭圆上的一点,若S△PF1A∶S△PF1F2=2∶1,则直线PF1的斜率为________.

因为椭圆的离心率为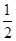 ,所以e=
,所以e= =
=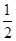 ,即a=2c,则A(0,b),F2(c,0),
,即a=2c,则A(0,b),F2(c,0),
设直线PF1的斜率为k(k>0),则直线PF1的方程为y=k(x+c),因为S△PF1A∶S△PF1F2=2∶1,即S△PF1A=2S△PF1F2,即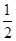 ·|PF1|·
·|PF1|·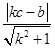 =2×
=2×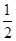 ·|PF1|·
·|PF1|· ,所以|kc-b|=4|kc|,解得b=-3kc(舍去)或5kc,又a2=b2+c2,即a2=25k2c2+c2,所以4c2=25k2c2+c2,解得k2=
,所以|kc-b|=4|kc|,解得b=-3kc(舍去)或5kc,又a2=b2+c2,即a2=25k2c2+c2,所以4c2=25k2c2+c2,解得k2= ,所以k=
,所以k= .
.
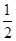 ,所以e=
,所以e= =
=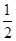 ,即a=2c,则A(0,b),F2(c,0),
,即a=2c,则A(0,b),F2(c,0),设直线PF1的斜率为k(k>0),则直线PF1的方程为y=k(x+c),因为S△PF1A∶S△PF1F2=2∶1,即S△PF1A=2S△PF1F2,即
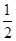 ·|PF1|·
·|PF1|·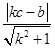 =2×
=2×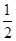 ·|PF1|·
·|PF1|· ,所以|kc-b|=4|kc|,解得b=-3kc(舍去)或5kc,又a2=b2+c2,即a2=25k2c2+c2,所以4c2=25k2c2+c2,解得k2=
,所以|kc-b|=4|kc|,解得b=-3kc(舍去)或5kc,又a2=b2+c2,即a2=25k2c2+c2,所以4c2=25k2c2+c2,解得k2= ,所以k=
,所以k= .
.
练习册系列答案
相关题目
 和
和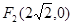 ,长轴长为6,设直线
,长轴长为6,设直线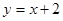 交椭圆C于A、B两点,求线段AB的中点坐标
交椭圆C于A、B两点,求线段AB的中点坐标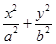 =1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( ).
=1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( ).



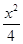 +y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF2|=( ).
+y2=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF2|=( ).


 ,
, 为坐标原点.若
为坐标原点.若 为椭圆上一点,且在
为椭圆上一点,且在 轴右侧,
轴右侧, 为
为 轴上一点,
轴上一点, ,则点
,则点




 ,左右焦点分别为
,左右焦点分别为 ,
, ,过
,过 两点,若
两点,若 的最大值为8,则
的最大值为8,则 的值是( )
的值是( )



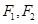 是双曲线
是双曲线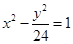 的两个焦点,
的两个焦点, 是双曲线与椭圆
是双曲线与椭圆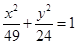 的一个公共点,则
的一个公共点,则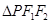 的面积等于_________.
的面积等于_________. 为椭圆
为椭圆 上的点,
上的点,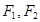 是其两个焦点,若
是其两个焦点,若 ,则
,则 的面积是 .
的面积是 .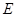 的方程为
的方程为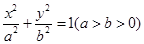 ,
,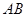 是它的一条倾斜角为
是它的一条倾斜角为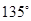 的弦,且
的弦,且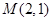 是弦
是弦