题目内容
2．已知向量$\overrightarrow{p}$=（2，-3），$\overrightarrow{q}$=（x，6），且$\overrightarrow{p}$∥$\overrightarrow{q}$，则x的值为（ ）| A． | 4 | B． | -4 | C． | 9 | D． | -9 |
分析 直接利用向量的平行的充要条件，通过坐标运算求解即可．
解答 解：向量$\overrightarrow{p}$=（2，-3），$\overrightarrow{q}$=（x，6），且$\overrightarrow{p}$∥$\overrightarrow{q}$，
可得-3x=12，解得x=-4．
故选：B．
点评 本题考查向量的坐标运算，向量的平行的充要条件的应用，考查计算能力．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
13．
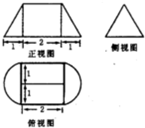一个几何体的侧视图是边长为2的正三角形，正视图与俯视图的尺寸如图所示，则此几何体的表面积为（ ）
一个几何体的侧视图是边长为2的正三角形，正视图与俯视图的尺寸如图所示，则此几何体的表面积为（ ）| A． | 12+2$\sqrt{3}$+3π | B． | 12+3π | C． | $\frac{\sqrt{3}π}{3}$+2$\sqrt{3}$ | D． | $\sqrt{3}$π+2$\sqrt{3}$ |
11．下列说法中，正确的是（ ）
| A． | 命题“若ax2＜bx2，则a＜b”的逆命题是真命题 | |
| B． | 命题“x=y，则sinx=siny”的逆否命题为假命题 | |
| C． | 命题“p且q”为假命题，则命题“p”和命题“q”均为假命题 | |
| D． | 命题“?t∈R，t2-t≤0”的否定是?t∈R，t2-t＞0 |
12．已知α，β是两个平面，直线l?α，l?β，若以①l⊥α，②l∥β，③α⊥β中两个为条件，另一个为结论构成三个命题，其中 正确的命题是（ ）
| A． | ①③⇒②，①②⇒③ | B． | ①③⇒②，②③⇒① | C． | ①②⇒③，②③⇒① | D． | ①③⇒②，①②⇒③，②③⇒① |