题目内容
13．
一个几何体的侧视图是边长为2的正三角形，正视图与俯视图的尺寸如图所示，则此几何体的表面积为（ ）| A． | 12+2$\sqrt{3}$+3π | B． | 12+3π | C． | $\frac{\sqrt{3}π}{3}$+2$\sqrt{3}$ | D． | $\sqrt{3}$π+2$\sqrt{3}$ |
分析 由三视图可知，此几何体为组合体，左右两侧为半圆锥，中间为三棱柱，从而求面积．
解答 解：由三视图可知，
此几何体为组合体，
左右两侧为半圆锥，中间为三棱柱，
左右两侧的半圆锥可合为一个圆锥，
其表面积为π×12+$\frac{1}{2}$×2×2π=3π；
中间的三棱柱三个侧面在表面，
其面积为3×2×2=12；
故此几何体的表面积为3π+12；
故选B．
点评 本题考查了学生的空间想象力与计算能力，属于基础题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
3．
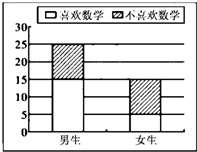对某中学高二某班40名学生是否喜欢数学课程进行问卷调查，将调查所得数据绘制成二堆条形图如图所示．
（Ⅰ）根据图中相关数据完成以下2×2列联表；并计算在犯错误的概率不超过多少的前提下认为“性别与是否喜欢数学课程有关系”？
（Ⅱ）从该班所有女生中随机选取2人交流学习体会，求这2人中喜欢数学课程的人数X的分布列和数学期望．
参考公式：K2=$\frac{（a+b+c+d）（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
临界值附表：
对某中学高二某班40名学生是否喜欢数学课程进行问卷调查，将调查所得数据绘制成二堆条形图如图所示．（Ⅰ）根据图中相关数据完成以下2×2列联表；并计算在犯错误的概率不超过多少的前提下认为“性别与是否喜欢数学课程有关系”？
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
参考公式：K2=$\frac{（a+b+c+d）（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
临界值附表：
| P（K2≥k0） | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
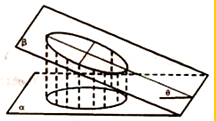如图，一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截，其截面是一个椭圆Γ，以该椭圆Γ的中心为原点，长轴所在的直线
如图，在矩形ABCD中，AB=2BC，E为线段AB的中点，将△ADE沿直线DE翻折成△A′DE，使平面A′DE⊥平面BCD，F为线段A′C的中点．