题目内容
10.设直线x-2y+1=0的倾斜角为α,则cos2α+sin2α的值为$\frac{8}{5}$.分析 根据直线x-2y+1=0的方程求出tanα的值,把cos2α+sin2α化成$\frac{{cos}^{2}α+2sinαcosα}{{sin}^{2}α{+cos}^{2}α}$,再用正切函数表示即可.
解答 解:∵直线x-2y+1=0的倾斜角为α,
∴tanα=$\frac{1}{2}$
∴cos2α+sin2α=$\frac{{cos}^{2}α+2sinαcosα}{{sin}^{2}α{+cos}^{2}α}$
=$\frac{1+2tanα}{{tan}^{2}α+1}$
=$\frac{1+2×\frac{1}{2}}{{(\frac{1}{2})}^{2}+1}$
=$\frac{8}{5}$.
故答案为:$\frac{8}{5}$.
点评 本题考查了直线方程的倾斜角与斜率的应用问题,也考查了三角函数求值的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知向量$\overrightarrow{p}$=(2,-3),$\overrightarrow{q}$=(x,6),且$\overrightarrow{p}$∥$\overrightarrow{q}$,则x的值为( )
| A. | 4 | B. | -4 | C. | 9 | D. | -9 |
20.在等差数列{an}中,a3=5,a4+a8=22,则{$\frac{1}{{{a_n}•{a_{n+1}}}}$}的前20项和为( )
| A. | $\frac{40}{41}$ | B. | $\frac{20}{41}$ | C. | $\frac{42}{43}$ | D. | $\frac{21}{43}$ |
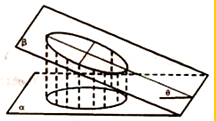 如图,一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截,其截面是一个椭圆Γ,以该椭圆Γ的中心为原点,长轴所在的直线
如图,一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截,其截面是一个椭圆Γ,以该椭圆Γ的中心为原点,长轴所在的直线 如图,在矩形ABCD中,AB=2BC,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.
如图,在矩形ABCD中,AB=2BC,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.