题目内容
12.设△ABC的内角A、B、C所对的边分别为a、b、c,且2$\sqrt{2}$(sin2A-sin2C)=(a-b)sinB,$\frac{c}{sinC}$=2$\sqrt{2}$(1)求角C;
(2)求△ABC面积的最大值.
分析 (1)由题意和正弦定理求出sinA、sinB、sinC,代入已知的式子化简,再由余弦定理求出cosC的值,即可求出角C的值;
(2)由(1)和条件求出c,利用余弦定理列出方程,化简后利用基本不等式求出ab的最大值,代入△ABC面积的公式求出最大值.
解答 解:(1)由题意和正弦定理得,$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2\sqrt{2}$,
则sinA=$\frac{a}{2\sqrt{2}}$,sinB=$\frac{b}{2\sqrt{2}}$,sinC=$\frac{c}{2\sqrt{2}}$,
代入2$\sqrt{2}$(sin2A-sin2C)=(a-b)sinB得,
a2-c2=ab-b2,即a2+b2-c2=ab,
由余弦定理得,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
又0<C<π,则C=$\frac{π}{3}$;
(2)由(1)可得,$\frac{c}{sin\frac{π}{3}}=2\sqrt{2}$,则c=$2\sqrt{2}×\frac{\sqrt{3}}{2}$=$\sqrt{6}$,
代入a2+b2-c2=ab可得,a2+b2-6=ab,
即ab+6=a2+b2≥2ab,解得ab≤6,当且仅当a=b时取等号,
所以△ABC面积S=$\frac{1}{2}absinC$=$\frac{\sqrt{3}}{4}$ab≤$\frac{\sqrt{3}}{4}×6$=$\frac{3\sqrt{3}}{2}$,
即△ABC面积的最大值是$\frac{3\sqrt{3}}{2}$.
点评 本题考查了正弦、余弦定理,三角形的面积公式,以及基本不等式求最值问题,属于中档题.

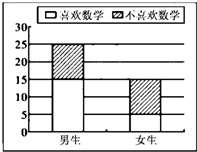 对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.
对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.(Ⅰ)根据图中相关数据完成以下2×2列联表;并计算在犯错误的概率不超过多少的前提下认为“性别与是否喜欢数学课程有关系”?
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
参考公式:K2=$\frac{(a+b+c+d)(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值附表:
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
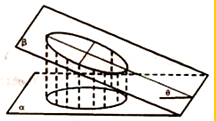 如图,一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截,其截面是一个椭圆Γ,以该椭圆Γ的中心为原点,长轴所在的直线
如图,一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截,其截面是一个椭圆Γ,以该椭圆Γ的中心为原点,长轴所在的直线