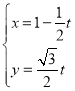题目内容
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点F的距离
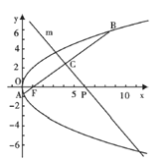
到焦点F的距离![]() ,倾斜角为α的直线经过焦点F,且与抛物线交于两点A、B。
,倾斜角为α的直线经过焦点F,且与抛物线交于两点A、B。
(1)求抛物线的标准方程及准线方程;
(2)若α为锐角,作线段AB的中垂线m交x轴于点P。证明:![]() 。
。
【答案】(1)抛物线的方程为![]() ,准线方程为
,准线方程为![]() (2)见解析
(2)见解析
【解析】
(1)根据抛物线的定义,求得![]() ,由此求得
,由此求得![]() 点坐标,将其代入抛物线方程,解方程求得
点坐标,将其代入抛物线方程,解方程求得![]() 的值,进而求得抛物线方程及其准线方程;(2)设出直线
的值,进而求得抛物线方程及其准线方程;(2)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 方程和抛物线方程,写出韦达定理,由此求得线段
方程和抛物线方程,写出韦达定理,由此求得线段![]() 中点坐标,进而求得线段
中点坐标,进而求得线段![]() 中垂线方程,由此求得
中垂线方程,由此求得![]() 点坐标,求出
点坐标,求出![]() ,由此计算出
,由此计算出![]() .
.
解:(1)由抛物线的定义知,![]()
将点![]() 代入
代入![]() ,得
,得![]() .得
.得![]()
∴抛物线的方程为![]() ,准线方程为
,准线方程为![]()
(2)证:设直线AB与直线m的交点为C.![]() .直线
.直线![]()
由![]() ,消去x得:
,消去x得:![]() 。
。
则
![]()
设线段AB中垂线m的方程为:![]()
令![]() ,得:
,得:![]() ,则点
,则点![]()
![]()
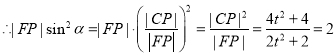

【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱,现统计了连续![]() 天的售出和收益情况,如下表:
天的售出和收益情况,如下表:
售出水量 |
|
|
|
|
|
收益 |
|
|
|
|
|
(1)若每天售出![]() 箱水,求预计收益是多少元?
箱水,求预计收益是多少元?
(2)期中考试以后,学校决定将诚信用水的收益,以奖学金的形式奖励给品学兼优的特困生,规定:特困生考入年级前![]() 名,获一等奖学金
名,获一等奖学金![]() 元;考入年级前
元;考入年级前![]() 名,获二等奖学金
名,获二等奖学金![]() 元;考入年级
元;考入年级![]() 名以后的特困生不获得奖学金。甲、乙两名学生获一等奖学金的概率均为
名以后的特困生不获得奖学金。甲、乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() .
.
①在学生甲获得奖学金的条件下,求他获得一等奖学金的概率;
②已知甲、乙两名学生获得哪个等第的奖学金是相互独立的,求甲、乙两名学生所获得奖学金总金额![]() 的分布列及数学期望
的分布列及数学期望
附:
【题目】为了调查中学生每天玩游戏的时间是否与性别有关,随机抽取了男、女学生各50人进行调查,根据其日均玩游戏的时间绘制了如下的频率分布直方图.

(1)求所调查学生日均玩游戏时间在![]() 分钟的人数;
分钟的人数;
(2)将日均玩游戏时间不低于60分钟的学生称为“游戏迷”,已知“游戏迷”中女生有6人;根据已知条件,完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
非游戏迷 | 游戏迷 | 合计 | |
男 | |||
女 | |||
合计 |
附: (其中
(其中![]() 为样本容量).
为样本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】下表表示的是某款车的车速与刹车距离的关系,试分别就![]() ,
,![]() ,
,![]() 三种函数关系建立数学模型,并探讨最佳模拟,根据最佳模拟求车速为120km/h时的刹车距离.
三种函数关系建立数学模型,并探讨最佳模拟,根据最佳模拟求车速为120km/h时的刹车距离.
车速/(km/h) | 10 | 15 | 30 | 40 | 50 |
刹车距离/m | 4 | 7 | 12 | 18 | 25 |
车速/((km/h) | 60 | 70 | 80 | 90 | 100 |
刹车距离/m | 34 | 43 | 54 | 66 | 80 |