��Ŀ����
����Ŀ��ijѧУΪ����ȫ��ѧ��Ϊ����ѧ�������С�һԪǮ��һƬ�ģ�������ˮ�����ѧ���ڹ�ˮ��ÿ��ȡһƿ��Ȫˮ�����Ծ�������������Ͷ��һԪǮ����ͳ��������![]() ����۳���������������±���
����۳���������������±���
�۳�ˮ�� |
|
|
|
|
|
���� |
|
|
|
|
|
��1����ÿ���۳�![]() ��ˮ����Ԥ�������Ƕ���Ԫ��
��ˮ����Ԥ�������Ƕ���Ԫ��
��2�����п����Ժ�ѧУ������������ˮ�����棬�Խ�ѧ�����ʽ������Ʒѧ���ŵ����������涨�������������꼶ǰ![]() ������һ�Ƚ�ѧ��
������һ�Ƚ�ѧ��![]() Ԫ�������꼶ǰ
Ԫ�������꼶ǰ![]() ��������Ƚ�ѧ��
��������Ƚ�ѧ��![]() Ԫ�������꼶
Ԫ�������꼶![]() ���Ժ������������ý�ѧ�𡣼ס�������ѧ����һ�Ƚ�ѧ��ĸ��ʾ�Ϊ
���Ժ������������ý�ѧ�𡣼ס�������ѧ����һ�Ƚ�ѧ��ĸ��ʾ�Ϊ![]() ������Ƚ�ѧ��ĸ��ʾ�Ϊ
������Ƚ�ѧ��ĸ��ʾ�Ϊ![]() ������ý�ѧ��ĸ��ʾ�Ϊ
������ý�ѧ��ĸ��ʾ�Ϊ![]() .
.
����ѧ����ý�ѧ��������£��������һ�Ƚ�ѧ��ĸ��ʣ�
����֪�ס�������ѧ������ĸ��ȵڵĽ�ѧ����������ģ���ס�������ѧ������ý�ѧ���ܽ��![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����
����
���𰸡�(1) ��������![]() Ԫ.
Ԫ.
(2) ��![]() ;�ڷֲ��м�������
;�ڷֲ��м�������![]() ��Ԫ��.
��Ԫ��.
����������������1�����ù�ʽ���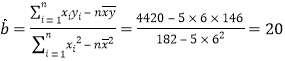 �ɵ�
�ɵ�![]() ���Ӷ�����ع鷽�̣���
���Ӷ�����ع鷽�̣���![]() ���뼴�ɵý������2�������¼�
���뼴�ɵý������2�������¼�![]() Ϊ��ѧ����ý�ѧ�𡱣��¼�
Ϊ��ѧ����ý�ѧ�𡱣��¼�![]() Ϊ��ѧ�����һ�Ƚ�ѧ�𡱣���
Ϊ��ѧ�����һ�Ƚ�ѧ�𡱣���![]() ���ɵý�����ڵ�ȡֵ����Ϊ
���ɵý�����ڵ�ȡֵ����Ϊ![]() �����ö����¼��ĸ��ʹ�ʽ�����Ӧ��
�����ö����¼��ĸ��ʹ�ʽ�����Ӧ��![]() ��ֵ�������ֲ��к�����ֵ����.
��ֵ�������ֲ��к�����ֵ����.
��⣺��1��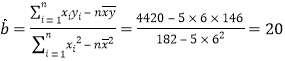
![]()
����![]()
��![]() ʱ��
ʱ��![]() ��Ԫ��
��Ԫ��
��ij���۳�![]() ��ˮ��Ԥ��������
��ˮ��Ԥ��������![]() Ԫ
Ԫ
��2�������¼�![]() Ϊ��ѧ����ý�ѧ�𡱣��¼�
Ϊ��ѧ����ý�ѧ�𡱣��¼�![]() Ϊ��ѧ�����һ�Ƚ�ѧ�𡱣���
Ϊ��ѧ�����һ�Ƚ�ѧ�𡱣���
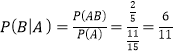
��ѧ����ý�ѧ��������£����һ�Ƚ�ѧ��ĸ���Ϊ![]()
��![]() ��ȡֵ����Ϊ
��ȡֵ����Ϊ![]()
![]()
![]()
![]()
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ����ѧ������
����ѧ������
 ��Ԫ��
��Ԫ��

����Ŀ��ij��Ⱥ�и���Ѫ�͵�����ռ�ı������±���
Ѫ�� | A | B | AB | O |
��Ѫ�͵�����ռ�ı���/% | 28 | 29 | 8 | 35 |
��֪ͬ��Ѫ�͵��˿��Ի�����Ѫ��O��Ѫ���Ը���һ��Ѫ�͵�����Ѫ���κ��˵�Ѫ���������AB��Ѫ���ˣ�������ͬѪ�͵��˲��ܻ�����Ѫ.����Ⱥ�е�С����B��Ѫ����������Ҫ��Ѫ���ʣ�
��1������һ���ˣ���Ѫ�������С���ĸ����Ƕ��٣�
��2������һ���ˣ���Ѫ�������С���ĸ����Ƕ��٣�
����Ŀ�������������ı�����Ϊ������ʱ���������Ļ������ǡ����ʢ�ģ���˱���������Ƕ���Ը��ȥ�������Σ�������һ�ݻ���ٻ����ṩ����ƽ������ͳ�Ʊ�.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 17.3 | 17.9 | 17.3 | 15.8 | 13.7 | 11.6 | 10.06 | 9.5 | 10.06 | 11.6 | 13.7 | 15.8 |
��1���������ͳ�Ʊ��ṩ�����ݣ�Ϊ������е���ƽ����������һ������ģ�ͣ�
��2������Ȼ���²�����13.7��ʱ������������������Σ��Ը�������ȷ���ĺ���ģ�ͣ�ȷ��������е��������ʱ��.